이전 글에 이어서. 사실 나는 확률론과 통계학이 정확하게 나눠지는 지점도 잘 모른다. 모른다고 지나칠 수는 없는, 쓰이는 개념들이 많아 울며 겨자먹기로 정리할 뿐..
일단 내가 통계에 해당하는 부분을 지금부터 정리하려고 한다.
확률에 관해서도 마찬가지이지만, 통계에 대해서는 특히나 기본적인 토대가 부족해서 그런지 명쾌하게 범주를 나누는 것을 잘 못하겠다. 그래도 많이 나오는 개념들에 대해서는 알고는 있어야 할테니, 일단 아는대로 개념들을 정리해보자.
모집단, 모수, 추정량..
통계학을 통해 현실 세계에서 흔히 우리가 알고 싶어하는 것은 바로 모집단이다. 알고 싶어하는 것을 모집단에 둔다고 하는 게 더 맞을 지도 모르겠다. 또 예시를 들어보자. 우리는 우리나라에 존재하는 모든 사람들의 키를 알고 싶다. 그러니 이걸 모집단으로 두자. 근데, 내가 알고 싶다고 해서 정말 전국을 누비며 사람들의 키를 잴 수는 없는 노릇이다. 시간적으로든, 비용적으로든, 우리가 직접 알아내는 것은 아무튼 모종의 이유 등으로 불가능하기 때문에 우리는 대안을 선택한다! 바로 표본을 뽑는 것. 가령, (이것도 사실 힘들 것 같지만) 전국민을 일렬로 세워두고 유한한 정도의 n명 정도만을 무작위로 뽑아서 키를 재는 것 정도는 가능할지도 모른다. 그래서 얻게 된 데이터를 통해 우리는 모집단의 어떤 값들을 추정할 수 있을 것이다. (참고로 절대 모집단 자체를 알 수는 없다. 모집단을 안다는 것은 우리가 정말 모집단 그 자체를 헤집어서 조사한다는 의미이다.) 이때 우리가 표본을 통해 추정해내는 어떤 값들을 모수(모집단의 평균이라던가, 분산이라던가)라고 부른다. 그렇다면 그냥 표본만 있으면 알아서 모수들이 뚝딱 나오나? 아니다. 우리는 표본을 가지고 평균을 구하거나 분산을 구하는 식으로 쪼작쪼작거린다. 그렇게 쪼작거리게 되는 값들을 추정량이라고 부른다.
평균, 분산, 표준편차
많은 개념들이 나왔다. 이 참에 범주적인 개념들 말고 가장 많이 만지게 될 핵심 개념들도 살펴보자.
평균! 평균은 모르는 사람이 거의 없겠지.. 단순히 모든 값들을 더하고 그것을 그 값들의 개수로 나눈 것. $E()$로 표기한다. 다른 말로 기대값이라고도 하는데, 엄밀하게는 조금 관점의 차이가 있는 용어라고 하지만 크게 상관은 없을 듯하다. 그렇다면 분산은 대체 뭘까? 분산은 데이터들이 평균으로부터 떨어져 있는 정도를 나타내며 $V()$로 표기한다. 평균은 모든 값들의 중앙 정도를 뜻하는 거니까, 분산이 크다면 데이터들은 넓게 산재해있을 것이고 작다면 데이터들이 밀집되어 있으렷다. 분산은 어떻게 구할까? 데이터들이 평균으로부터 떨어져 있는 정도라 했으니 단순하게 데이터값에서 평균을 빼면 되겠지? 그러면 그것들로 또 평균을 내면 될 것이다! 이때 문제가 발생한다.
$\large X = \{1,2,3,4,5\}$
가 있다고 생각해보자. 이때 평균은 무엇일까?
$\large E(X) = \frac{1}{n}\sum_{i=1}^{n}x_i = \frac{1+2+3+4+5}{5} = 3$
그러면 분산을 구하기 위해 이 평균인 3을 각 값에서 빼고 그것을 평균을 내려해보자.
$\large \frac{(1-3) +(2-3)+(3-3)+(4-3)+(5-3)}{5} = 0$
이게 바로 문제다! 단순하게 값들에서 평균을 빼준 뒤(참고로 이렇게 그냥 평균을 뺀 것을 편차라 부른다.)에 평균을 내려니 분자식이 0이 되어버린다. 이때 우리는 꼼수를 부린다. 평균과 떨어져 있는 거리를 알고 싶다면, 그 값을 그냥 빼나, 빼서 제곱을 하나 상관이 그다지 없다. 그러나 그것으로 얻게 되는 효과는 모든 값이 양수로 바뀌어 상쇄되는 값이 없어진다는 것.
$\large V(X) = \frac{1}{n}\sum_{i=1}^{n}(X-E(X))^2 = \frac{(1-3)^2 +(2-3)^2+(3-3)^2+(4-3)^2+(5-3)^2}{5} = 2$
이게 바로 분산이다. 우리는 이 분산을 보고 데이터들이 얼마나 산재해 있는지를 얼추 판단할 수 있게 된다.
마지막으로 표준편차도 우리는 많이 들어본다. 실제로는 이 값을 평균과 떨어진 지표로 더 많이 활용하는데, 분산을 제곱했던 게 거슬려서! 라고 보면 되시겠다.표준편차는 단순하게 분산에 제곱근을 씌우면 된다.
$\large \sigma(X) = \sqrt{V(X)}$
어쩜 이리 쉬울 수가!
표본
위에서 우리는 표본이 뭔지 얼핏 들어서 알고 있다. 이것에 대한 제대로 된 정의를 짚는 것보다, 이것에서 나오는 각종 재미있는 특성들을 아는 게 중요하다.
다시 모집단이니 표본이니 하는 이야기로 돌아가보자. 내가 우리나라에 있는 모든 사람들을 줄세워 놓고, 무작위로 n명을 뽑아 표본을 만들려고 한다. 그럼 이 표본 속 사람들의 키의 평균을 낼 수 있을 것이다. 이것은 표본의 평균이니 표본평균이라 부를 수 있다. 마찬가지로 표본분산도 있다. 근데, 이거 했으니까 끝인가? 우리는 무작위로 어쩌다 한번 뽑은 사람들로 우리나라 사람들의 전체 키의 평균을 알 수 있다고 말할 수 있을까? 절대 아니다. 우리가 무작위로 뽑은 사람의 태반이 어쩌면 영유아들일지도 모르잖냐. 아 그럼 어쩔 거냐~ 여기에 대해 우리에게는 조금 더 수고롭긴 해도 여전히 모집단을 다 뒤집어 엎는 것보다는 나은 방법이 있다. 바로 이런 표본을 많이 뽑는 것이다. 우리는 여기에서 복원추출로(뽑힌 사람이 또 뽑힐 수도 있게, 그래야 찐 무작위니까) 계속 뽑아나갈 것이다.
이렇게 많은 표본들을 뽑았다. 아까 n명씩 뽑아서 각 표본들을 만들었으니 그러한 m개의 표본이 생겼다고 쳐보자. 이 많은 표본들을 각각 표본평균을 낼 수 있을 것이다. 그러면 이때, 우리는 이 표본평균들로 또 평균을 낼 수 있다. 무슨 소리냐? 우리에게는 m개의 표본이 있으니 m개의 표본평균이 있을 것이다. 이 표본평균들을 다 더한 뒤에 m으로 나누는 작업을 해볼 수 있다는 것이다! 이를 표본평균의 평균이라고 한다. 이게 뭐지, 싶겠지만 나중에 중요하게 된다. 신기하게도 표본평균을 뭔가 쪼작거리면 재밌는 일들이 일어난다.
표본과 관련된 몇가지 공식들
자, 일단 우리가 알고 싶어하는 게 뭐다? 모집단이다. 실질적으로 모집단을 아는 것은 불가능해서, 우리는 표본의 추정량을 사용해서 모집단의 모수들이라도 알고 싶다. 보통 우리는 모수로서 모집단의 평균과 분산, 모평균$\mu$과 모분산$\sigma^2$을 알고자 한다(이 기호들에 익숙해질 필요가 있다. 왜 모분산이 시그마인지는 모르겠다.. 표준편차랑 헷갈리게). 이제 우리는 여기에서 재밌는 일을 겪는다! 일단 X에서 추출한 표본을 $\bar{X}$라고 표기한다는 것을 알아둘 필요가 있다.(미리 말하는데 여기 있는 내용들은 수식적으로 증명이 가능하다. 근데 그것까지 하지는 않으려고 한다.)
$\large E(\bar{X}) = \mu$
헉~ 이게 뭔 소리냐~ 표본평균의 평균이 모평균과 같다! 그럼 분산도 그럴까? 분산은 또 다르다.
$\large V(\bar{X}) = \frac{\sigma^2}{n}$
아까와 다르게 n을 나눠줘야만 한다.
한편 표본평균을 쪼작거리느라 뒷전으로 밀려나 표본분산$S^2$도 재미있는 공식이 있다. 사실 재미없다.
$\large S^2= \frac{1}{n-1}\sum_{i=1}^{n}(X_i - \bar{X})^2$
바로 이것이다. 우리가 여태 알던 분산은 평균처럼 그냥 n을 나눠주면 되었는데, 이놈은 특이하게 n-1로 나눈다. 이것은 불편추정량을 만들기 위해서라는.. 고상한 이유가 있는데 그것까지 알 필요는 없을 것 같다.
중심극한정리
많이 알아봤는데, 이것도 알아봐야 한다.이전에 분포에 대한 언급을 많이 했다. 맨 처음에 확률분포가 뭔지도 이야기를 했는데, 확률분포는 사실 모양이 매우 다양하다.

말만 그런 게 아니라 정말 다양하다. 뭐, 하등 문과생이 이걸 어찌 다 알겠냐. 다만 하나 정도는 꼭 알아둘 필요가 있다. 바로 정규분포이다.

뭐 대충 이렇게 생긴 놈을 말한다. 가우시안 분포라고도 하는데, 아무튼 이 놈은 평균에서 확률이 가장 높고 양 옆으로 갈수록 확률이 낮아지는 모양을 하고 있다.
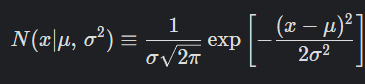
그 식을 보면 매우 복잡하게 생겼으나, 아무튼 이놈은 말처럼 뭔가 아주 표준이 되고 정규적인 느낌으로 쓰이는 분포이다. 이놈은 몇몇가지 특징이 있다. 딱봐도 알겠지만 평균을 기준으로 대칭이라던가, 하는 것들 말이다. 워낙에 중요한 분포라 저 함수식을 모르더라도, 모양이나 특징 같은 것은 알아두는 것이 좋다.
근데 이 놈을 왜 갑자기 내가 들먹이는가, 하니 아까 위에서 말했던 표본들과 연관이 된다. 어떤 모집단에서든 우리는 표본을 뽑을 수 있다. 복원추출로 뽑을 경우 우리는 정말 무한대로 뽑아낼 수 있을텐데, 이러한 표본들을 열라 뽑아내서 그 평균인 표본평균을 내면, 그 표본평균들의 집합은 정규분포를 따른다는 것이 바로 중심극한정리Central Limit Theorem이다. 이게 통계학의 근간을 이루는 정도의 정리라고 하는데, 나는 그런 거창한 것까지는 모르겠지만 여하튼 매우 신기한 놈이기는 하다. 모집단이 어떤 분포인지도 모른다. 또한 거기에서 뽑아낸 표본이 어떤 분포인지도 모른다. 그럼에도 아무튼 그런 표본들을 열라 뽑아내서 각 표본평균들을 모아서 그것을 집단으로 만들어내면, 그것은 정규 분포를 따른다는 것이다. 저 반듯한 산등성이 모양이 나온다는 것이다! 이것을 통해 통계학에서는 다양한 검정이나 추측을 할 수 있게 된다. (내 시절 한정인가..?) 고등학교 때 신뢰도 95퍼니, 신뢰도 99퍼니 해서 확률을 따지고 하는 게 다 이 놈에서 비롯되는 것이라고 할 수 있다. 통상 n이 30이 이상이면 성립한다고 본다던가, 그런 것들이 있는데, 너무 자세하게 들어가지는 말자.
벌써 너무 신기하고 재미난 것들을 쑤셔넣어서 머리가 아프려 한다!
'인공지능 in 네부캠 AI 4기 > 기초 & 이론' 카테고리의 다른 글
| 확률과 통계 for AI, Machine Learning(1) (0) | 2022.09.26 |
|---|---|
| 경사하강법(Gradient Descent) 구현(2) (0) | 2022.09.24 |
| 경사하강법(Gradient Descent) 구현(1) (0) | 2022.09.20 |