저번 글에 이어서..
조금 더 복잡한 선형 회귀
저번에는 정말 단순한 모양의 식을 세웠다. 미지수가 하나인 식에서 W와 b를 하나씩 찾아내면 되는 거였는데, 사실 이보다 더 거대하게 일을 키울 수도 있다.
$\Large y = w_0x_0 + w_1x_1 + ... +w_dx_d + b$
이런 식으로 x도 열라 많고, 그에 따른 가중치도 열라 많다면?! 보기만 해도 귀찮다.. 어디 보자.. w는 d+1개에 b 하나니까 우리가 구해야 하는 값의 갯수는 d+2개렷다. 그리고 이런 식으로 생긴 데이터가 대충 n개 들어오는 것이다.그러면 또 이 n개의 데이터를 오차 내서 제곱하고, 평균 내고.. 상상만 해도 귀찮다!
음, 실제로 계산해보면 매우 귀찮다. 그래도 차근차근 해봐야겠지.
일단 이러한 식들은 보통 행렬의 곱으로도 나타낼 수 있다.
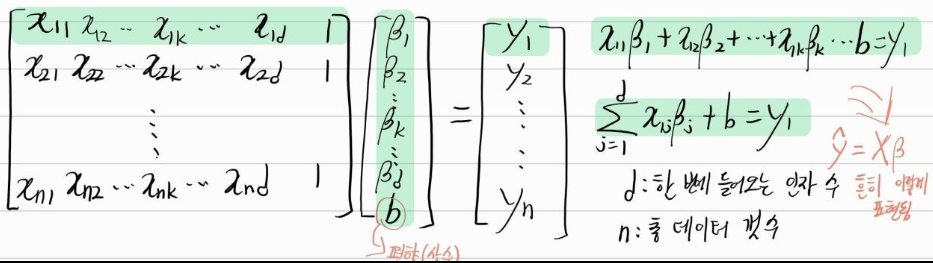
이런 식으로 말이다. 미리 말하지만, x행렬에서 굳이 따로 k열을 살려서 표기한 이유가 있다. 'k열'을 유심히 보라.
이제 본격적으로 풀어보도록 하자. 일단의 우리의 문제는 무엇인가? $\beta_i$를 구하는 것이다(표기의 귀차니즘으로 b는 생략한다. 있어도 없어도 결국 푸는 방식 자체는 똑같다.).
$\beta_i$를 구하기 위해서 우리는 똑같이 MSE를 사용할 것이다. 그래서 각 $\beta_i$에 대해 편미분을 진행해서 계속 경사하강법을 시행할 것이다!
d개의 베타 중에서 하나만 추출해서 일반화를 시켜보자. $\beta_k$에 대해 편미분을 한 값을 구해보자!
$\Large \partial_{\beta_k}(y-X\beta)^2\ =\ \partial_{\beta_k}\{ \frac{1}{n}\sum_{i=1}^{n}(y_i - \sum_{j=1}^{d}X_{ij}\beta_j)^2 \}$
이야.. 보기만 해도 어지럽다. 차근차근 보자면, 일단 식을 $\beta_k$에 대해 편미분하자는 것. 잘 보면 n과 d가 아까 위에 써넣은 그대로 들어가 있는 것을 확인할 수 있다. 1

이 정도로 간단한 식으로 정리하기까지 세 번의 시도를 거쳤고, 대략 3일이 소요됐다.이 정도면.. 충분히 정리가 잘 된 것 같다. 내 머릿속에 박제된 수학 지식의 범주 상에서 충분히 납득될 만한 증명이 완성됐다..! 자 그럼 다시 정리해보자.
(수정, $X^T$ 가 아니라 $X^T_k$가 정확하다. 즉, X행렬의 k열벡터를 전치시키라는 말이다.)
$\Large \partial_{\beta_k}(y-X\beta)^2\ = - \frac{2}{n}X^T_k(y-X\beta)$
이 정도로 매우 축약해 정리가 가능하다. 이러면 우리는 $\beta_k$에 대해 편미분한 값을 얻어낸 것이다. 즉, 모든 $\beta$에 대한 편미분을 간편하게 표기한다면 얼추 이런 모양을 띄고 있을 것이란 뜻이다!
$\Large \partial_{\beta}(y-X\beta)^2\ = - \frac{1}{n}X^T(y-X\beta)$
은근슬쩍 2도 나눠버렸는데, 이런 상수는 어차피 학습률에 의해서 상쇄되기에 가뿐히 제거하였다.
그럼 이제 코드로 이 식을 만나볼 시간이다.
for t in range(5000):
_y = train_x @ beta_gd - train_y
grad = np.transpose(train_x) @ _y / n_data
beta_gd -= 0.02 * grad엥! 매우 간단하다. 바로 위에 있는 식이 grad라는 변수에 담기고, 그것이 편미분값이니 그것을 통해 베타값을 계속 수정해나가고 있는 것이다.
참고로 @는 행렬 연산을 뜻하는 기호이고, beta_gd 변수는 1차원 리스트, 즉 벡터의 모양을 하고 있다.
상수인 편향 값을 생각한다면 x행렬에 1열을 추가하는 식의 추가 작업이 필요한데, 일단 개념을 이해하는데 중점을 두기 위해 그것은 생략했다.
급할수록 대충 가라.. SGD
지금까지 알아본 경사하강법은 주어진 데이터를 전부 활용한다. 전부 사용한다하여 Full Gradient Descent라고도 부르는데, 여기에 다른 방법이 있다. 결국 데이터들을 이용하기는 하는데, 반복문을 돌릴 때마다 몇 개씩만 무작위 추출하여 그것을 토대로 학습을 시키는 방식이다. 반복문이 돌아갈 때마다 무작위로 정해둔 갯수(보통 미니 배치mini-batch라고 부른다.)를 추출해서(대체로 비복원 추출) 그것으로 학습을 시킨다. 이를 확률적 경사하강법, 영어로는 Stochastic Gradient Descent라고 부른다. 흔히 SGD라는 용어를 접하게 된다면 이것을 뜻한다고 보면 된다.
방법도 간단하다. 말그대로 반복문 안에 비복원 무작위 추출을 걸어서 미니 배치를 만들고, 그것을 토대로 값을 갱신해나가면 끝난다. SGD는 간단한 수고를 더는 대신 많은 이점을 가진다.

일단, 경사가 완만해지는 속도가 조금 더 빠르다. 학습률로 걸어둔 제한을 선을 넘지 않은 한에서 간혹 가다 조금 더 크게 넘나들며 빠르게 극소점으로 수렴을 하게 된다.
또 이 점에서 착안해서, 확실한 극소점으로 갈 수 있다는 장점도 가진다.

값이 너무 조금씩 갱신되다 보면 중간에 위치한 고지를 넘지 못해 왼쪽의 진정한 극소점을 향할 수 없다. 그러나 SGD는 어쩌다가 확 튀는 값을 이용해 어쩌다가 저 고지를 넘어서 극소점에 다다를 수 있는 것이다.
무엇보다 당연히 연산 속도가 더 빠르다. 10000개의 데이터를 통해 10000번을 학습시키는 것보다는, 매번 무작위 100개의 데이터로 10000번을 학습시키는 게 훨씬 빠를 것이다.
물론 주어진 데이터 범위 내에 있기는 하지만 어디까지나 무작위로 추출하는 것이기 때문에 경우에 따라서는 극소점에 무조건 도달하지는 않을 것이다. 그러나 딥러닝에서는 SGD가 FGD보다 낫다는 것이 실증적으로 검증되었다고 한다. 그래서 실무에서는 SGD가 쓰이는 게 보통이다.
'인공지능 in 네부캠 AI 4기 > 기초 & 이론' 카테고리의 다른 글
| 확률과 통계 for AI, Machine Learning(2) (0) | 2022.09.26 |
|---|---|
| 확률과 통계 for AI, Machine Learning(1) (0) | 2022.09.26 |
| 경사하강법(Gradient Descent) 구현(1) (0) | 2022.09.20 |