Collaborative Filtering
줄여서 CF! 현업에서 굉장히 많이 쓰이는 기본적인 개념이며 그만큼 종류도 굉장히 다양하다.
협업 필터링은 '많은 유저들로부터 얻은 기호 정보'를 이용해 유저의 관심사를 예측하는 방법이다.
왜 협업(collaborative)인가? 집단, 다수의 의견을 활용하면서 이러한 전체적인 데이터가 많이 축적될수록 협업의 효과가 커지며 추천이 정확해질 것이란 가정을 두고, 이를 토대로 예측을 하기 때문이다.
이전 예시로 보자면 많은 사람들이 기저귀를 산 후에 맥주를 많이 샀다는 데이터를 토대로 기저귀를 사는 사람은 맥주에 대해 높은 평점을 부여할 것이란 예측을 할 수 있는 것이다.
이전에 추천시스템에서 다루는 문제가 Top k개를 줄세우고 그것을 추천하는 랭킹 문제와, 특정 유저가 특정 아이템에 대해 가질 선호도(or 평점, CTR)를 예측하는 예측 문제가 있다고 언급했다. 협업 필터링은 이중 예측 문제에 해당한다.
자세하게 말하자면 일단 주어진 선호도 데이터를 활용해 유저-아이템 행렬을 생성한다. 유저도 무수하긴 하지만, 일단 아이템이 무수하니 당연히 일개 유저들은 그 모든 아이템에 대한 구매 이력이나 선호도 정보가 없을 것이고, 이 행렬은 빈칸이 많은 매우 희소한 행렬이 될 것이다. 여기에서 유사도 기준을 정한 뒤, 그리고 그 유사도를 기반으로 하여 행렬에 비어있는 값들을 예측하여 채우는 것이 바로 협업 필터링의 방식이다.
행렬을 채우는 데에 있어 유저의 취향이나 아이템의 상세한 속성을 알 필요 없다는 것이 CF의 특징이다.
유사도는 뭐냐? 가령 두 유저가 둘 다 짜장면과 짬뽕을 선호하고 우리가 이 정보를 알고 있다고 해보자. 그럼 우리는 이 둘이 유사하다고 생각을 할 수 있고, 이중 한 유저가 탕수육을 좋아한다는 정보가 있을 때 다른 한 유저도 비슷한 정도로 선호한다고 예측할 수 있는 것이다. 유사도의 기준에 대해서는 이후 자세히 다룰 것이다.

보다시피 CF는 분야가 세분화되어 있다. 어차피 다 볼 것이지만 먼저 가장 고전적인, Neighborhood-based CF를 먼저 다뤄볼 것이다.
Neighborhood-Based Collaborative Filtering
무슨 말이냐, 이웃을 기반으로 한 협업 필터링! 말 그대로 유사한 이웃을 기준으로 예측을 하는 것을 말한다. 이 이웃은 유저가 될 수도, 아이템이 될 수도 있다.
참고로 이미 가지고 있는 데이터(메모리)를 사용한다해서 Memory-Based CF로도 불린다.
먼저 유저 기반 협업 필터링User-Based CF를 알아보자.

예시를 보면 우리가 구하고 싶은 것은 일단 유저 B가 스타워즈에 대해 내릴 평점이다. 이때 이 유저와 비슷한 평점을 내리는 유저가 있다. A는 전반적으로 B와 비슷하게 평점을 내렸으니 A를 연관된, 혹은 유사한 이웃으로 두고 평점을 예측하자!는 것이 바로 UBCF.

그렇다면 아이템을 이웃으로 두는 Item-Based CF는? 위의 표를 세로로 보는 것이다. 스타워즈와 비슷하게 평점을 받은 영화는 헐크와 아이언맨이 있으니 스타워즈에 대해 유저 B는 저 영화들과 비슷하게 평점을 내릴 것이라 예측할 수 있다.
이렇게 이웃을 기반으로 평점을 에측하는 것이 바로 NBCF이다.
개념이 그냥 이게 거의 전부라 할 정도로 매우 간단하게 구현이 가능한 모델이다.
그러나 두 가지 부분에서 문제가 발생한다. 이 문제는 비단 이 NBCF만의 문제가 아니라 추천시스템 전반에 걸친 문제로서 이를 해결하기 위해 이후 계속 개선된 모델이 나온 것이라고 보면 된다.
첫번째는 바로 규모 확장성Scalability이 떨어진다는 것. 현재 유투브에 얼마나 많은 영상과 유저가 있을까? 모든 것을 고려하면 행렬의 크기가 엄청나게 커질텐데 그것을 어떻게 다룰 것인가? 이는 이후 모델인 MF에서 보게 될 것.
두번째는 희소성Sparsity의 문제. 희소가치를 이야기하는 것이 아니라, 말 그대로 정보가 희소하다는 것이다. 넷플릭스에 있는 모든 작품들을 유저들이 보지는 않았을 것이다. 몇십만 개가 넘는 아이템들 중 끽해야 수백 개는 봤을까? 위에서도 언급했듯이 유저-아이템 행렬은 크기는 큰데 채워져 있는 부분은 매우 적은 희소 행렬sparse matrix의 모습을 하고 있을 것이고, 그런 적은 데이터를 토대로 예측을 하는 것은 쉬운 일이 아니다. 그래서 행렬 희소비율sparsity ratio가 99.5%가 넘어간다면 성능 저하 이슈로 이 모델을 적용하지 않는 게 좋다고 한다.
K-Nearest Neighbors CF
KNN CF. 이것은 NBCF에서 비롯되는 모델이다. 희소행렬과 규모 확장의 한계에 대응하는 모델로, 이웃 기반을 하기는 하는데 K 개(명)의 이웃만을 활용하는 기법이 바로 이 모델의 아이디어.

누가 가장 유사한지를 따지고, 유사하다고 볼 K의 양을 정해서 이웃 기반 CF를 하자는 것. 이 K는 하이퍼 파라미터로 바깥원을 사용한다면 초록 원은 파랑색과 유사하다고 생각될 것이다.
가령 실제로 스타워즈를 본 사람은 엄청 많을 것이다. 그러나 이 모두를 이웃으로 두지 않고 이중 유사하다고 생각되는 10명 정도의 데이터만 이용하겠다는 것이다.
Similarity Measure
우리는 유사한 K명을 랭킹지어야 하기에 이제 정말 유사도의 기준을 자세하게 뜯어볼 필요가 있다. 무엇을 기준으로 누가 유사하다고 평가할 것인가? 이걸 밝혀내야만 협업 필터링을 수행할 기반을 다질 수 있다.

사실, 방법은 다양하다. 두 점의 거리라고도 이야기할 수 있고, 두 집합의 교집합으로도 이야기할 수 있고, 분포를 그릴 수도 있고.. 유사도를 측정하는 다양한 방법이 있으며 조건과 상황에 맞춰 가장 좋은 성능을 보이는 측정법을 우리는 선택하면 한다.
직관적으로는 거리의 역수 개념이라 생각하면 편하다. 거리가 짧으면 그만큼 유사하다는 사고 방식(쿨백 라이블러 발산도 분포의 유사도를 측정하는데 거리로 표현되잖나).
추천 시스템에서 주로 사용되는 4가지 유사도 측정법을 살펴보자.
Mean Squared Difference Similarity
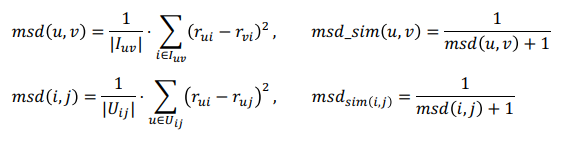
이것은 거의 추천시스템에서만 쓰이는 측정법으로 유저-아이템 행렬에서 유저가 내린 평점들의 차를 구한다. 그리고 그것을 제곱한 뒤에 전체 갯수로 나누기. 이름만 봐도 알겠지만 대충 MSE오차랑 비슷한 연산을 한다. 유클리드 거리와 비슷하다고도 말할 수 있는데, 아무튼 그것을 그다음 그걸 역수를 취해 유사도로 삼는다.
1을 더해주는 것은 분모가 0이 되는 것을 방지하는 smoothing 기법.
MSE처럼 유사할수록 차이는 작아질 것이고, 그것이 분모에 있기 때문에 유사도는 커진다고 말할 수 있다.
Cosine Similarity

코사인 유사도. 컨텐츠 기반 추천에서도 잠시 다뤘던 것으로, 벡터 간의 유사도를 측정하는 기법이다. 두 벡터의 차원이 같을 때 사용할 수 있는 기법으로, 두 벡터의 값이 많이 달라도 방향만을 토대로 유사도를 측정할 수 있어서 많이 쓰이는 측정법이다.
Pearson Similarity

피어슨 상관계수를 생각하면 된다. 각 벡터를 각 벡터의 표본평균으로 정규화를 시키고 코사인 유사도를 구하는 것. 이를 통해 얻는 것은 유저 간의 성향 차이를 보정하는 것. 가령 어떤 사람은 재밌으면 죄다 5점 때리고 재미없어도 3점을 때리지만, 누군가는 정말 재밌을 때만 5점, 아니면 죄다 1점을 때릴 수 있다. 이러한 유저 간의 차이를 고려할 수 있다는 것. 그래서 위의 코사인 유사도보다 성능이 더 무난하다.
Jaccard Similarity

자카드 유사도. 단순하게 합집합 분의 교집합으로 집합간의 유사도를 파악한다. 달리 말하면 두 집합의 공유도라고 할 수 있고, 완전히 같은 집합이라면 값은 1이 될 것이고 겹치는 것이 없다면 값은 0이 될 것이다.
이것은 차원이 같고 다르고의 여부가 상관 없다는 장점을 가지고 있다(장점이 맞나..? 어차피 행렬이면 차원은 고정인 것 같은데..).
이것은 아이템을 소비한 여부를 따져서 유저간의 유사도를 구할 때 쉽게 사용할 수 있는 방법이다.
적용
이제 본격적으로 이 NBCF를 적용하는 모습을 보자. KNN은 이웃한 K명을 고르는 문제이고 고르고 난 이후에는 NBCF와 다를 게 없다. 기본적으로 CF는 예측 문제임을 상기하라!
위에서 본 예시를 다시 사용해보자면,

저 물음표를 어떻게 채울 것이냐? UBCF의 관점에서 알아볼 것인데, IBCF도 결국 똑같기 때문에 따로 적지는 않겠다.
Absolute Rating
사실 가장 간단한 방법은 평균Average을 내는 것이다. 유저 B가 여태 내린 평점의 평균이든, 스타워즈에 내려진 평점의 평균이든.
그러나 어느 쪽으로든 만족스럽지는 않다. 유저를 기준으로 하면 해당 영화의 특수함을 조금도 고려하지 않는 꼴이고, 영화를 기준으로 하면 해당 유저의 평점으로 적절한 것인지 의심된다.

그래서 이를 조금 비틀어서 Weighted Average를 사용해 평점을 예측할 수도 있다. 가령 B는 A와 비슷하니 A의 평점과 비슷하면서, C와는 그다지 유사하지 않으니 C의 평점이 덜 반영되도록 평점을 예측해볼 수 있을 것이다.
그래서 일단 각 유저와의 모든 유사도를 구한다. 그 다음 그것을 분모 삼은 후 분자로는 유사도를 가중치로써 평점에 곱하여 더한다. 가중치를 고려한 평균인 것이다.
이러한 방법들은 절대적 평점absolute rating이라 부르는데, 이는 유저가 내린 평점을 그대로 활용하기 때문이다. 그러나 위에서 봤듯이 유저마다 평점을 주는 성향이 다를 수 있다. 어떤 유저는 어쩌다 개쩌는 것에 대해서만 5점을 주지만, 다른 유저는 5점을 퍼주는 스타일일 수도 있잖나. 전자의 5점이 조금 더 가치있게 평가되는 것이 바람직할 것이다. 우리는 그러한 유저 간의 편차를 반영하고 싶다.
Relative Rating
그래서 나오는 게 상대적 평점이다. 피어슨 유사도처럼 평균을 이용해 각 평점의 값을 빼서 정규화하는 작업을 거치는 것이다. 이를 통해 이 유저가 준 5점이 유저의 평균 평점으로부터 편차deviation가 어찌 되는지를 파악하고 이를 활용하는 것이다.

이제 우리는 정확하게 따지자면 평점이 아니라 그 평점의 편차로 예측을 하게 된다. 이 다음에는 아까 봤던 average나 weighted average를 쓰면 된다.

참고로 지금은 편차를 구하는 것이기 때문에 마지막에 해당 유저의 평균 평점을 더해주어야만 정확한 예측을 할 수 있다. 편차는 평균을 뺀 값이니까 편차를 구했으면 다시 평균을 더해서 정규화를 풀어줄 필요가 있는 것이다.
위에서 말했듯이 IBCF도 결국 방식은 똑같다.

Top-N Recommendation
자 이제 우리는 협업 필터링을 통해 유저-아이템 행렬을 채우는 방법을 알게 됐다! 명심할 것은 결국 우리는 추천시스템을 만들고 있다는 것이다.
이렇게 신나게 예측을 해서 행렬의 빈 칸을 채웠으면 이제 우리는 이를 토대로 예측 평점이 높은 아이템을 추천해주면 된다. Top-N recommedation이라 표현하는데, 그냥 랭킹 문제이다.
즉 예측 문제와 랭킹 문제로 추천시스템에서 다루는 요소를 나눴지만 결국에는 랭킹으로 환원된다는 것. 우리는 추천을 해주는 게 최종 목적이니까!
정리하자면 협업 필터링 자체는 예측 문제를 푸는 모델이다. 그리고 그 예측을 통해 행렬을 완성하면 Top-N recommendation이라 부르면서 이를 통해 랭킹 문제를 해결하는 것!
'인공지능 in 네부캠 AI 4기 > 추천시스템' 카테고리의 다른 글
| Item2Vec & ANN (0) | 2022.10.24 |
|---|---|
| 모델 기반 협업 필터링 (0) | 2022.10.23 |
| 컨텐츠 기반 추천 (0) | 2022.10.18 |
| 연관분석 (0) | 2022.10.15 |
| 인기도 기반 추천 (0) | 2022.10.11 |