목차

본 글은 확률 및 랜덤 프로세스 강의의 교재인 "Probability, Statistics, and Random Process for Electrical Engineering"를 읽고 강의 내용과 함께 정리한 내용을 담고 있다. 사실 한글 교재가 있는데 그것을 내가 pdf로 구하는 것을 실패(...)한 관계로 그냥 영어로 읽는다. 이 책의 목차는 다음과 같으며 현재 다루고 있는 파트는 밑줄 표시했다.
예제 문제들이 있다. 해당 문제들은 따로 글을 작성하여 정리를 해둔다.
- Probability Models in Electrical and Computer Engineering
- Basic Concepts of Probability Theory
- Discrete Random Variables
- One Random Variable
- Pairs of Random Variables
- Vector Random Variables
- Soums of Random Variables and Long-Term Averages
- Statistics
- Random Processes
- Analysis and Processing of Random Signals
- Markov Chains
- Introduction to Queueing Theory
이번 장의 내용은 기초적인 확률 이론의 개념들을 다룬다. 이전 장에서 넌지시 나왔던 사건, 표본이니 하는 것들이 여기에서 정리가 될 것이다. 사실 고등학교 수준에서 배우는 확률 수준보다도 더 근본적인 수준의 내용이 나오는데, 이 내용들이 이후 장들에서 더 정교해지고 커가는 것을 우리는 보게 될 것이다.
우리가 이 장을 통해 볼 것은 크게 이렇다. 집합이론, 표본 공간, 사건, 확률 공리, 조건부 확률, 독립, 연속 실험
2.1 Specifying Random Experiments 랜덤 실험 구체화
이전 장에서 우리는 수학적 모델로서 확률론적 모델과 결정론적 모델을 짧게 비교했다. 확률론적 모델은 무작위성이 있는, 랜덤한 실험에 대해서 적용된다. 그럼 이 랜덤한 실험이 뭘까?
랜덤한 실험은 같은 조건에서 해당 실험이 반복되더라도 결과(outcome)를 예측할 수 없는 실험을 말한다.
다음이 랜덤한 실험의 예시이다. 이 실험들은 이번 장에서 계속 이용될 예정이기 때문에 어떤 실험인지 대충 외워둔 상태로 읽으면 도움이 된다. 여기에서 기록한다(note)는 말이 바로 확률적으로 볼 실험의 내용이다. 다른 표현으로 적힌 실험들도 있지만, 결국 다 측정하거나 재거나 그런 뜻이다!
- E1 : 1부터 50까지의 숫자가 적혀 있는 공이 들어간 주머니에서 공을 하나 꺼낸다. 그 공에 적힌 숫자를 기록한다.
- E2 : 1부터 4까지의 숫자가 적혀 있는 공이 들어간 주머니가 있다. 1,2가 적힌 공은 검은색, 3,4가 적힌 공은 하얀색이다. 여기에서 공을 하나 꺼내고 그 공에 적힌 숫자를 기록한다.
- E3 : 동전을 차례대로 세번 던진다. 앞면과 뒷면이 나온 순서를 기록한다.
- E4 : 동전을 차례대로 세번 던진다. 앞면의 개수를 기록한다.
- E5 : 이전 장에서 봤던 음성 패킷 전송 시스템. N명의 대화자가 있다. 10ms 단위 초에서 오로지 침묵 상태만이 담긴 패킷의 개수를 기록한다.
- E6 : 잡음이 많이 낀 채널에서 정보 블록이 에러 없이 전달될 때까지 반복적으로 블록을 전송한다. 필요한 전송 횟수를 센다.
- E7 : 0부터 1 사이의 랜덤한 숫자를 뽑는다(실수).
- E8 : 웹 서버에서 페이지 요청 간 시간을 측정한다.
- E9 : 특정 환경에서 메모리 칩의 수명을 측정한다.
- E10 : $t_1$ 시간의 오디오 신호 값을 결정한다.
- E11 : $t_1$, $t_2$ 사이의 오디오 신호값들을 결정한다.
- E12 : 0부터 1 사이의 랜덤한 숫자를 두 개 뽑는다(실수).
- E13 : 0부터 1 사이의 랜덤한 숫자를 두 개 뽑는다(실수). 이때 첫번째 X를 뽑고 난 후, 0과 X 사이에 랜덤한 숫자를 뽑는다.
- E14 : 시간 $t=0$에 시스템 요소가 설치된 후 작동되고 있다. 시스템이 작동하고 있는 시간 t에서 $X(t) = 1$이고, 시스템이 고장난 이후의 시간 t에서는 $X(t) = 0$이다.
랜덤 실험에서는 무엇이 측정 대상인지 정확하게 특정하는 진술이 필요하다. 당장 3,4는 굉장히 비슷한 내용을 다루지만 엄밀하게는 다르다. 여기에 어떤 실험은 연속적인 내용을 다루는 것도 있고 어떤 실험은 부분실험으로 쪼갤 수도 있다. 이번 장에서 조금 자세하게 보게 될 것이다!
The Sample Space 표본 공간
랜덤 실험에서는 항상 같은 결과가 나오지 않기 때문에 나올 수 있는 결과들의 집합을 따질 수 있다.
먼저 결과(outcome) 혹은 표본점(sample point)를 더 작게 분해할 수 없는 결과(result)라고 해보겠다. 우리나라 말로 하면 둘다 그냥 결과라서 말이 헷갈리는데, 요컨대 대체로 outcome을 많이 쓰기 때문에 앞으로 결과라고 하면 굳이 따로 표기하지 않는 이상 outcome이라 생각하면 된다. 아무튼 표본점이라고도 불리는 이 결과는 한 실험에 하나만 발생한다. 그렇기에 각 결과는 상호 배제적이다. 이 말은 동시에 일어날 수 없다는 뜻이다.
그리고 가능한 모든 결과들의 집합을 표본 공간 S라고 부른다. 그러니 표본 공간 S를 가진 실험이 있다고 했을 때 이 실험의 결과는 곧 표본 공간 S의 원소라는 뜻이다. 이를 또 다르게 표현하면, 표본 공간 S에서 한 원소를 뽑는 것은 해당 랜덤 실험을 한번 진행하여 결과를 기록하는 것과 같다.
표본 공간을 간단하게 이해할 수 있는 예시는 단순하게 주사위를 던지는 경우로 생각해보면 된다. 주사위를 던져 나올 수 있는 눈의 개수는 총 6가지이다. 이때의 표본 공간 S는 $S = {1,2,3,4,5,6}$라는 것이다.

위 예시들의 표본 공간(일일히 쓰기 귀찮다..). 흔히 표본 공간은 집합을 표현하는 방식으로 표현된다. 집합 표현 방식은 대충 다 알 테니까 넘어가도록 하겠다.
그보다 더 따져야 하는 것은, 표본 공간은 원소의 특징으로부터 유한, 가산 무한, 무한이라는 세 가지 유형이 있다는 것이다.
유한은 말 그대로 집합의 원소의 개수가 유한하다는 것이다. 주사위 같은 것 해당된다고 보면 된다.
가산 무한은 무한이지만 그럼에도 원소를 하나씩 세는 시도를 할 수 있는, countable한 무한을 말한다. 주사위를 던지는데 주사위의 눈이 1이 나올 때까지 계속 던지는 실험을 생각해보자. 주사위를 던진 횟수를 기록할 것이다. 간단하게 생각하면 6번 중에 1번은 나올 테니까 금방 끝나겠지만, 어쩌다가 정말 1이 계속 안 나올 수도 있을 것이다. 이때 횟수는 분명하게 세어볼 수 있음에도 이 실험의 표본 공간은 무한하다.
무한은 정확하게는 셀 수 없는 무한이라 해야겠지만, 아무튼 실수 영역의 원소를 가졌을 때 무한이라고 한다. 0부터 1 사이의 아무 수를 뽑는다고 생각해보면, 우리는 정확하게 원소의 개수를 세는 것이 불가능하다. 한 원소 다음에 어떤 원소가 올지 가늠할 수도 없다.
이 표본 공간의 유형은 앞으로 종종 활용될 것이다. 당장은 유한과 가산 무한한 원소를 가질 때 이산 표본 공간, 무한일 때는 연속 표본 공간이라 부른다는 것만 알면 된다.

연속 표본 공간의 경우 좌표 공간을 통해 보이는 것이 간편하다. 두 수를 골라야 하는 경우에는 보다시피 2차원 공간에 표현이 되고 있다.
Event 사건
자, 이제 우리는 랜덤 실험에 대해 전체 가능한 모든 결과의 집합인 표본 공간을 알게 됐다. 그런데 우리는 가능한 모든 결과가 궁금한 게 아니다. 주사위를 던졌을 때 3이 나올 확률이 궁금하다던가, 짝수의 눈이 나올 확률이 궁금한 것이다. 다시 말해 우리는 가능한 결과 중 특정한 결과들에 관심을 가진다. 그럼 우리는 표본 공간 S의 부분집합에 관심을 가진다는 말과 같다.
이렇게 표본 공간의 부분집합을 가르켜 사건이라고 한다.


이것들이 위 예시들의 사건의 일부이다.
조금 특별하게 봐야 할 사건이 둘 있다.
전사건(certain event)은 모든 결과의 집합을 말한다. 즉, 표본 공간 S를 말한다.
이 반대인 공사건(null event) $\emptyset$도 있다. 말 그대로 어떤 결과도 포함하지 않는 집합, 절대 일어나지 않는 사건이다.
그리고 한 결과만을 원소로 가지는 사건은 근원 사건(elementary event)이라고 부른다.
잠시 정리를 해보자.
- 결과(outcome) : 더 분해될 수 없는 결과(result)
- 표본 공간 : 가능한 모든 결과의 집합. 원소의 특성에 따라 이산, 연속으로 나뉜다.
- 사건 : 표본 공간의 부분 집합
- 전사건 : 모든 결과의 집합(표본 공간을 사건으로 표현한 것)
- 공사건 : 결과를 포함하지 않는 집합
- 근원 사건 : 하나의 결과를 원소로 가지는 집합
Review of Set Theory 집합 이론 리뷰
우리는 앞으로 사건을 논하면서 집합 표현을 많이 쓰게 될 것이다. 그러니 집합 이론을 되짚을 필요가 있다!
진짜 간단한 용어 정의부터.
집합은 대상의 모음(collection of obj)이다. 그리고 대문자로 쓴다.
가능한 모든 대상을 담고 있는 집합을 전체 집합(universal set)이라 하며 흔히 U라고 표기한다. 랜덤 실험의 관점에서는 전체 집합이 곧 표본 공간이다. 즉 U = S.
그럼 집합의 대상들을 뭐라고 부르는가? 흔히 원소(element), 점(point)이라 부른다. 점이라는 표현은 해당 집합이 무한일 때 부르는 표현이다! 통상적으로는 원소라 부른다. 원소는 소문자로 표기한다.
$\large x \in A,\ y \notin A$
이러한 표현은 x가 집합 A의 원소이고, y는 집합 A의 원소가 아니라는 뜻이다.
$\large A \subset B$
집합에 대해 성립하는 기호로 A가 B의 부분집합이라는 뜻이다.
부분집합(subset)은 A의 모든 원소가 B에도 속한다는 뜻이다.
정리하다가 알게 된 건데 부분집합이 아니라는 기호는 따로 없는 모양이다..? 찾아보니까 진짜 따로 정의되지 않은 모양이다. 비슷한 검색들이 바로 연관되어 올라오는 것 보니까 나만 이런 생각한 게 아닌 듯하다.
여튼, 만약 부분집합이 아니라는 표현이 필요한 경우에는 저 기호에 사선으로 작대기를 하나 그어서 표시를 하겠다(정의가 따로 없는 모양이니 이건 내 정의다!).
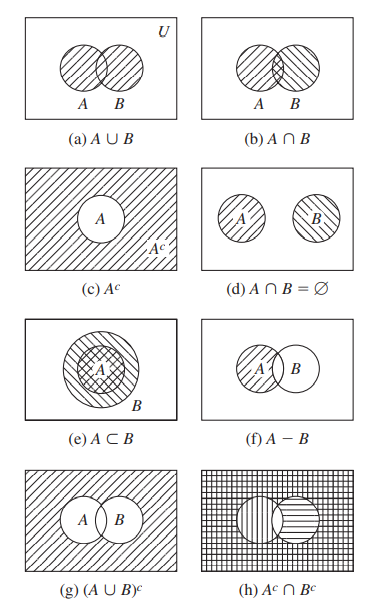
집합을 가장 흔하게 표현하는 방법, 벤 다이어그램. 전체 집합을 직사각형으로 그리고 그 안에 다른 집합들을 넣는다.
$\large 임의의\ 집합\ A에\ 대하여\ \emptyset \subset A$
공집합(empty set) $\emptyset$은 원소가 없는 집합으로 정의된다. 그리고 공집합은 모든 집합의 부분집합이다.
$\large A = B \Leftrightarrow A \subset B\ and\ B \subset A$
두 집합이 같다는 말은 서로 정확히 같은 원소를 가지고 있다는 것을 뜻한다. 그리고 이를 돌려말하면 서로가 서로의 부분집합이라는 말이기도 하다. 보통 두 집합이 같음을 보일 때 쓰는 가장 표준적인 방법이 서로가 서로의 부분집합이라는 게 성립하는 것을 보이는 것이다. 그리고 두번째 방법이 각 원소가 같다는 것을 보이는 것.
여기까지 아주 기본적인 정의와 기호를 살펴봤다. 이제는 세 가지 기본 연산자를 보자.
$\large A \cup B = \{x : x \in A\ or\ x \in B\}$
이 기호는 합집합(union)을 뜻하며 A 또는 B에 속하는 원소들의 집합을 뜻한다. 여기에서는 '또는'은 논리적 합을 말한다. 4
$\large A \cap B = \{x : x \in A\ and\ x \in B\}$
이 기호는 교집합(intersection)을 뜻하며 A 그리고 B에 동시에 속하는 원소들의 집합을 뜻한다. 여기에서 '그리고'는 논리적 곱을 말한다. 만약 이것이 공집합이라면? 두 집합은 서로소(disjoint), 배반 관계라는 것을 뜻한다.
$\large A^c = \{x : x \notin A\}$
이 기호는 여집합(complement)을 뜻하며 A에 속하지 않는 원소들의 집합을 뜻한다. 논리적 부정에 해당하는 표현이다.
$\large S^c = \emptyset\ and\ \emptyset^c = S$
가 성립한다. 전사건과 공사건은 서로의 여집합이다!
$\large (A^c)^c = A$
이것도 알아두자. 어디까지나 전부 정의에서 도출되는 개념들이다.
여기까지가 기본적인 세 가지 집합 연산자이다. 여기에 추가적으로 한가지만 더 보자면
$\large A - B = \{x: x\in A\ and\ x\notin B\} = A \cap B^c $
바로 차집합(difference)! A에는 속하면서 B에는 속하지 않는 원소들의 집합을 뜻한다.
위의 기본 연산자들의 정의에 따라 이 표현은 A와 B의 여집합의 교집합이 된다.
또한 $B^c = S \cap B^c = S - B$도 성립한다는 것을 염두해 두자.
이 책 웃긴 게.. 4개 알려줘놓고 계속 3개가 기본 연산자랜다. 일단 내가 딱 봐도 기본이 되는 3개를 내가 정해서 썼다. 차집합은 다른 연산자의 정의로 정의가 가능하니까 이게 맞겠지.
기본 연산자들에 대해서는 다음과 같은 속성들이 성립한다.
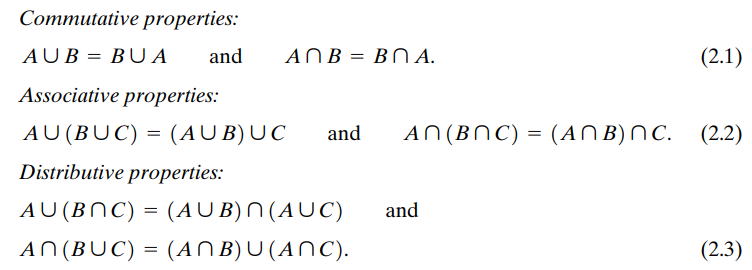

순서대로 교환 법칙(commutative properties), 결합 법칙(associative properties), 분배 법칙(distributive properties), 드모르간의 법칙(demorgan's rules)이다. 아주 기본적인 내용들이라 굳이 더 다루지는 않겠다. 참고로 드모르간의 법칙은 벤 다이어그램을 통해 증명된다.
$\large \cup^n_{k=1}A_k = A_1 \cup A_2 \cup \cdots \cup A_n\\
\large \cap^n_{k=1}A_k = A_1 \cap A_2 \cap \cdots \cap A_n$
합집합과 교집합은 반복될 수 있다. 이를 가산 합집합, 가산 교집합이라 부른다.
Event Classes 사건 모임
클래스, 모임. 이 개념은 너무 어렵다.. 검색을 해봐도 제대로 찾기도 힘들고, 뭐 어쩌라는 건지 싶은 내용의 느낌이다. 대충 알아본 바로는, 러셀의 역설을 피하기 위해 나온 개념이란 것 같기도 하다. 이게 진짜 내용이 산으로 가는 게, 이거 이후로 보렐 필드나 이런 내용들도 나오는데 이건 보니까 위상수학과 관련된 내용이라나 뭐라나.. 이렇게까지 변화구를 던지는 이유가 있을 거 아닙니까.. 일단 책 내용을 이야기하기 이전에 내가 찾은 내용으로 간단하게 정리해보겠다. 이해가 잘 안 돼서 확실하지는 않다.
일단 모임(class)은 집합을 아우르는 상위 개념이다. 집합이 이 개념에 포함되는 것으로, 집합이 가지는 특성(중복은 없고, 순서 고려되지 않고, 자기 자신을 포함하고 어쩌고..)을 보면 사실 집합이라는 것은 제한적인 모임이라고 생각할 수 있다.
모임은 그냥 대상들의 모임일 뿐, 그 자체로는 제대로 정의되지 않는다. 포함관계를 가지는 어떤 것이다.
Mathematics | 왜 하필 Borel Set일까? - 하우론브레인 Inc. (tistory.com) 책 내용상에서는 이보다 한번 더 나아가야만 한다. 어차피 이후에도 한번 더 설명이 나오니까 이 글을 그때 같이 읽어보기로 한다.
대충 이 정도만 개념 잡고 다시 책을 읽어보자.
표본 공간 S는 모든 가능한 결과의 집합이다. 그리고 사건은 S의 부분집합이다.
이때 우리는 관심있는 사건들을 모아 모임 F를 만들 수 있다. 이 모임 안에 존재하는 사건만이 확률을 부여받는다. 그리고 이 F 속에서 이뤄지는 집합 연산을 통해 만들어지는 사건들 역시 F 속에 있다.
유한, 가산 무한에서 이것을 보이는 것은 쉬운 일이다. 그런데 무한에서는 F가 S의 모든 부분집합을 가지면서 확률의 공리를 따르게 할 수 없다. 현실에서는 교차점과 가산 합집합으로 모든 사건을 얻어낼 수 있다. 우리는 이러한 사건 모임을 보렐 영역(Borel field)이라 부른다.
모임이란? 집합들의 모음이다.
유한 표본 공간 S의 모든 부분집합을 일컬어 멱집합(power set)이라 한다. 멱집합은 원소 n개가 있는 표본 공간에 대해 $2^n$개의 원소 개수를 가진다. 이건 생각해보면 당연하다.
위 내용이 책에서 설명한 내용인데, 이것만 보고 무슨 소리인지 어떻게 알 수 있을까..?
또 한편으로 책에서 하는 말은 기초적인 단계에서 이정도 이상으로 알 필요가 없다고 한다. 그럴거면 말을 꺼내지도 말던가.. 한껏 궁금하게 만들고 몰라도 된다니?
아무튼 나는 아직 제대로 개념을 모르겠어서 예를 들어가면서 설명할 수가 없다. 이 개념은 이후에 다시 보게 될테니 여기에서 넘기겠다.
2.2 The Axioms of Probability 확률의 공리
확률이 뭐냐? 한 실험이 수행되었을 때 그 사건이 얼마나 일어날 것 같은지(likely)를 나타내는 숫자이다.
확률 법칙(probability law) 상에서는 사건 모임 F에 속하는 사건들에 대해 확률이 부여될 수 있다. 아무튼 확률 법칙이란 것은 사건에 숫자를 부여하는 함수인 것이다. 우리는 이전 장에서 상대도수의 속성을 본 적이 있다. 그리고 확률의 공리는 확률 법칙을 통해 이 상대도수의 속성들을 물려받게 된다.
일반화된 정의를 보자.
표본 공간 S와 사건 모임 F를 가진 랜덤 실험 E가 있다. E를 위한 확률 법칙은 F에 속하는 사건 A에 P[A]라는 숫자를 할당하는 법칙이며, 이 숫자는 A의 확률이라 부른다. 또한 이 확률은 다음의 공리를 만족한다.

공리 3이 둘로 나뉜다. 첫번째는 유한 표본 공간에서, 두번째는 가산 무한 표본 공간에서 성립한다. 실질적으로 후자가 전자를 포함하고 있다고 보더라도 무방하다. 유한 표본 공간에서도 성립하는 공리여야 하기에 저렇게 따로 표기가 될 뿐이다.
사실 이미 상대도수에서 본 개념들이라 어렵지 않다! 그리고 매우 직관적이고 단순하다. 확률이 0 이상이고, 전체 확률은 1이 될 것이고, 서로 배반(서로소, 상호 배제. 같이 일어나지 않음)인 경우 합집합의 확률이 각각의 확률의 총합과 같다.
자, 이제 여기에서 몇가지 정리들을 이끌어내보자.

어떤 집합과 그 여집합의 합집합은 전체집합이라는 것을 이용한다.

이 증명은 모든 확률이 1 이하라는 것을 드러낸다. 그러니 모든 확률은 결국 0이상 1이하 사이에 있다는 뜻이다.

공사건의 확률은 0이다.

공리 3이 가산 합집합에도 성립한다는 것을 나타낸다. 수학적 귀납법을 사용한다.

합집합의 확률에 대한 일반화. 전부 배반사건으로 쪼갠 다음 재결합시킨다. 결국 합집합은 아무리 커도 두 집합의 합보다 작거나 같다는 것도 의미한다.
사실 이렇게 귀찮게 하는 것보다 벤 다이어그램을 쓰면 더 편하게 증명할 수 있다.
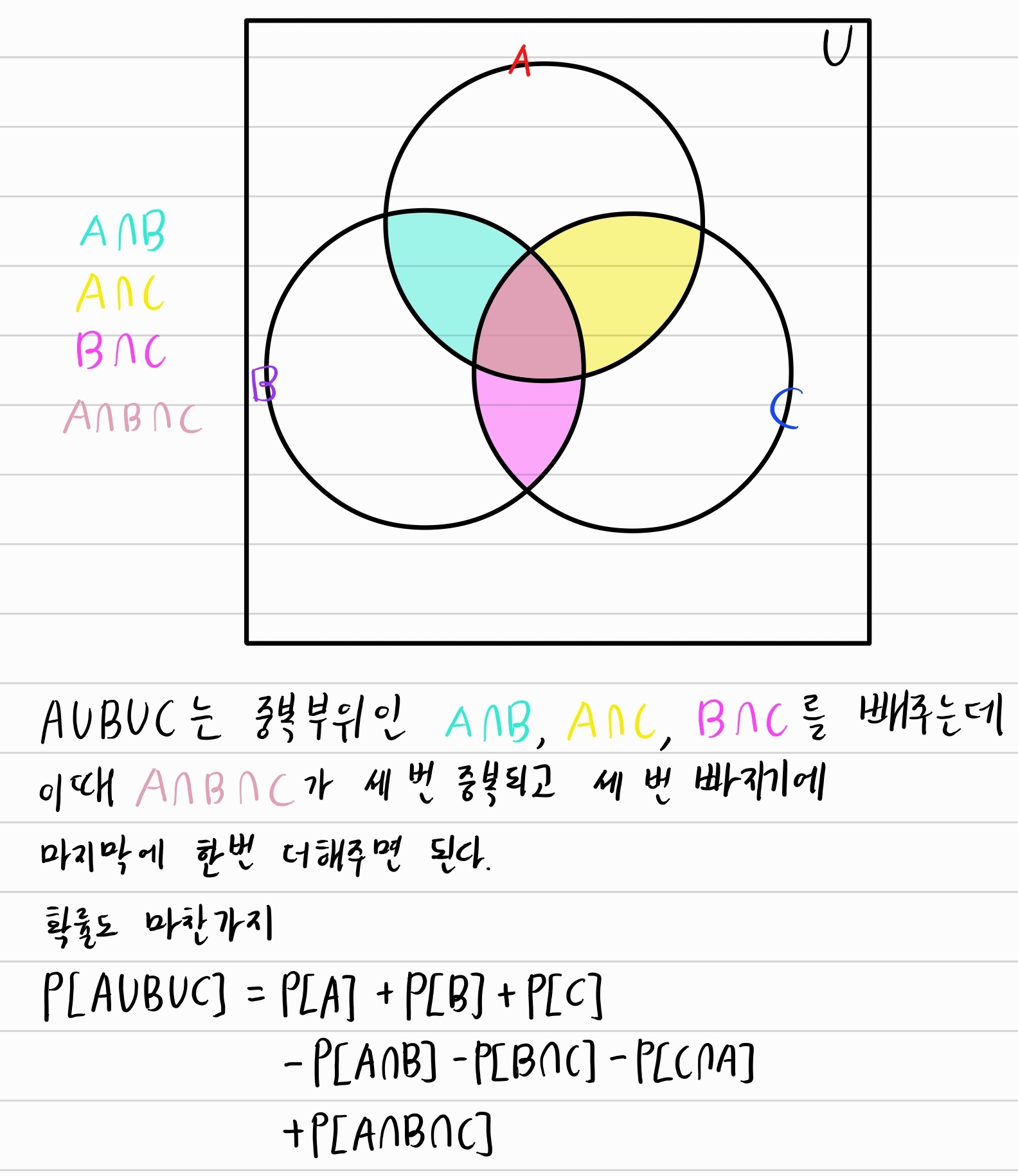
가령 세 집합의 합집합에 대해 벤 다이어그램을 통해 증명한다면 이렇게 증명할 수 있다. 이때 보면 어떤 패턴이 있는 것을 알 수 있다. 차수에 계속 음수 양수를 바꿔가면서 표현되는 합집합의 확률에 대해서(사실 정확하게는 합집합의 원소의 개수에 대해서) 포함-배제 원리(inclusion-exclution principle)라고 부른다. 어떤 교집합은 포함하면 다음 교집합은 배제하고를 반복하기에 붙은 이름이다.


위의 것을 일반화시킨 증명. 이게 참 어려워서 조금 찾아봤다. 포함-배제 원리의 세 가지 증명 – I Seul Bee 증명에는 다양한 방법이 있으나 책에서 귀납법으로 해보라길래 도전해본 것.
이거 하느라 3일 정도 묶여 있었던 것 같다.. 접근법은 얼추 알고 있었는데, 수식을 푸는 과정에서 연산이 잘 안 돼서 힘들었다.
참고로 이항 계수는 바로 다음 절에서 나온다! 이항 계수에 대해 모른다면 다음 글을 읽고 다시 오는 게 편할 것이다.

마지막 증명은 부분집합이 상위 집합보다 작다는 것을 의미한다.
이러한 증명들을 통해 우리는 다양한 사건들의 확률을 알아낼 수 있다!
그렇지만 결국 초기에 확률 할당이 이뤄져야만 이 공리와 증명들을 활용하여 다른 사건들의 확률도 알아낼 수 있는 것이다. 요컨대 사건 A의 확률을 알아야만 이를 통해 A의 여집합이나 이런 것들을 알 수 있게 된다는 것!
이제 이 초기 확률 할당을 하는 방법, 그 법칙을 알아보러 가보자.
Discrete Sample Spaces 이산 표본 공간
표본 공간의 유형 별로 확률을 할당하는 법칙(probability law)가 다르다. 일단 만만한 이산 표본 공간에 대해 알아보자.
이산 표본 공간에서는 각각 하나의 결과를 담는 근원사건이 있다. 한 번의 실험에 한 결과만 나오기 때문에 당연히 각 근원사건은 서로 배반(동시에 일어날 수 없음)이며, 또한 해당 표본 공간의 어떤 사건이든 근원 사건을 단위 삼아 나타내어진다.

즉, 한 사건의 확률은 그 사건의 결과, 또는 근원 사건 수의 총합으로 나타낼 수 있다는 것과 같다. 그것이 바로 유한 공간에서의 확률 법칙! 요컨대 이산 표본 공간에서는 근원 사건에 대해 확률만 부여해주면 만사 OK라는 것이다.
여기에서 만약 표본 공간 속 각 결과가 나올 가능성이 전부 같다면,

이러한 법칙이 성립한다. 주사위를 한번 던져 나오는 눈을 기록하는 실험이라면 표본공간 $S = {1,2,3,4,5,6}$일 것이고, 각 결과는 동일하게 일어날 가능성을 가지기에(equally likely) 각 근원 사건의 확률은 $\frac{1}{6}$이 된다는 뜻이다.
참고로 유한 표본 공간이 전부 이런 식으로 확률을 나타낼 수 있는 것은 아니다! 주사위를 두 개 던져서 나오는 눈의 총합을 실험으로 삼는다면 각 근원사건은 나올 가능성이 동일하지 않다. 아무래도 2, 12보다는 6이 더 많이 나오게 될 것이다.

교재에서 나온 예시를 빌려써보겠다. 보다시피 표본공간은 {0,1,2,3}인데, 이때 앞면의 개수가 2일 확률이 단순하게 $\frac{1}{4}$는 아니라는 것은 딱 봐도 알 수 있을 것이다.
이전에 우리는 모임(class)라는 개념을 통해서 모임에 속하는 사건들만이 확률을 부여받는다고 말한 적 있다. 확실하지는 않지만, 어쩌면 이런 것과 연관되는 것일지도 모르겠다.
가산 무한 표본 공간 역시 근원 사건에 대해 확률을 부여하는 식으로 사건들의 확률을 다룰 수 있다. 책에는 예제와 함께 설명하지만, 구태여 더 설명하지는 않겠다. 어차피 결국 요지는 이산 표본 공간에서는 가장 작은 단위에서 확률을 부여하겠다는 말이다.
Continuous Sample Spaces 연속 표본 공간
연속 표본 공간이라 한다면, 실수 R의 영역이 가장 대표적이라 할 수 있겠다. 위 개념을 따라가면 우리는 표본 공간 S의 모든 부분 집합을 가진 모임을 통해 확률을 부여해야 한다. 근데 여기에서는 모든 부분 집합이란 말이 모호하다. 이때 나오는 게 보렐 영역 개념인데, 뭐, 요지는 실수의 영역에서 모든 닫히고 열린 구간을 포함하며, 또 그 구간 간의 집합 연산을 하더라도 여전히 해당 나와바리를 벗어나지 않는 영역이라는 것이다. 이 덕분에 우리는 확률을 부여하는 것이 가능해진다.
이 공간에 대해서 우리는 어떻게 확률을 부여할 수 있는가? 단순하게 생각하면, 그림을 그려서 확률을 부여하면 된다.

이런 식으로 말이다. 여기에서 분명하게 알아야할 점은, 연속 표본 공간에서의 확률은 한 점에 대해서 부여하지 않는다는 것이다. 사실 부여할 수는 있다. 위 그림에서 $x= \frac{1}{2}$일 확률을 구해보자. 점은 크기가 없기 때문에 면적이 존재하지 않고, 따라서 확률은 0이다. 일반화하자면 특정한 점에 대한 확률은 전부 0이다! 어쩌면 이상하게 느껴질지도 모르지만, 무한이라는 공간에서의 한 점은 0에 가깝다는 것을 생각하면 또 그렇게 말도 안 되지는 않는다.
그렇기에 연속 표본 공간에서는 구간(interval)의 확률을 구하는 것이 중요한 요건이 된다.
'학교 공부 > 확률및랜덤프로세스' 카테고리의 다른 글
| 3. Discrete Random Variables(이산 확률 변수) (0) | 2023.03.31 |
|---|---|
| 2. Basic Concepts of Probability Theory(확률 이론의 기초 개념) ... 3 (0) | 2023.03.22 |
| 2. Basic Concepts of Probability Theory(확률 이론의 기초 개념) ... 2 (0) | 2023.03.22 |
| 1. Probability Models in Electrical and Computer Engineering(전기, 컴퓨터 엔지니어링에 쓰이는 확률 모델) (0) | 2023.03.16 |