2. Basic Concepts of Probability Theory(확률 이론의 기초 개념) ... 2

 

 

목차

 

본 글은 확률 및 랜덤 프로세스 강의의 교재인 "Probability, Statistics, and Random Process for Electrical Engineering"를 읽고 강의 내용과 함께 정리한 내용을 담고 있다. 사실 한글 교재가 있는데 그것을 내가 pdf로 구하는 것을 실패(...)한 관계로 그냥 영어로 읽는다. 이 책의 목차는 다음과 같으며 현재 다루고 있는 파트는 밑줄 표시했다.

예제 문제들이 있다. 해당 문제들은 따로 글을 작성하여 정리를 해둔다. 

1. Probability Models in Electrical and Computer Engineering
2. Basic Concepts of Probability Theory
3. Discrete Random Variables
4. One Random Variable
5. Pairs of Random Variables
6. Vector Random Variables
7. Soums of Random Variables and Long-Term Averages
8. Statistics
9. Random Processes
10. Analysis and Processing of Random Signals
11. Markov Chains
12. Introduction to Queueing Theory

내용이 너무 많아져서 글을 나눴다. 

2.3 Computing Probabilities Using Counting Methods 계수법을 통한 확률 계산

확률의 공리와 각종 증명들, 그리고 확률을 부여하는 과정에 대해서 알아보았다. 그렇다면 잠시 유한 표본 공간에 한정하여, 그것도 모든 결과가 동일하게 나오는(equiprobable) 유한 표본 공간에 대하여 경우의 수를 세는 방법을 알아보자. 순열, 조합 등의 이야기를 해보겠다는 것이다.
이게 왜 필요한가? 주사위를 3번 던지는 상황을 상상해보자. 그리고 나오는 눈 순서를 전부 기록할 것이다. 이때 표본 공간 S의 크기는 어떻게 될까? 6가지 결과가 나오는 주사위가 3번 던져지니까 6을 세 번 곱하면 그게 전체 경우의 수이고 곧 표본 공간의 크기일 것이다. 곱의 법칙이라고도 하는데, 이런 것들을 제대로 알고 넘어가야 계산이 용이해진다.

책에서는 나오지 않는 것 같은데, 잠시 곱의 법칙이 뭔지도 보자. 곱의 법칙은 두 사건이 동시에 일어나고 각 사건에서의 경우의 수가 m과 n일 때, 전체 경우의 수는 그 곱과 같다는 법칙이다. 앞에서도 계속 이 개념을 써먹고 있었기에 사실 더 전에 써놨어야 했을 것 같기도 한데, 어려운 개념은 아니니까 넘어가자..

순서를 고려하는 것과 복원의 여부로 4가지의 상황을 나눌 수 있고, 각각 n개에서 k개를 뽑는 경우의 수는 다음과 같다.
!는 팩토리얼을 뜻한다. 왜 이런 경우의 수가 나오는지 아래에서 보게 될 것이다.

Sampling with Replacement and with Ordering 순서를 고려한 복원 추출

n개에서 k개를 뽑는다. 이때 꺼낸 것은 다시 집어넣을 것이고, 차례대로 뽑을 것이다. 이 말은 매번 새롭게 뽑는 행위를 k번 반복하겠다는 말과 같다. 그리고 매 행위마다 n개 중에서 뽑을 것이기 때문에 n가지 경우의 수에서 하나 뽑는 행위를 k번 하겠다는 뜻이다. 
이 경우 전체 경우의 수는

$\large n^k$
이다.

Sampling without Replacement and with Ordering 순서를 고려한 비복원 추출

이번에도 n개에서 k개를 뽑을 것이다. 그렇지만 이번에는 복원을 하지 않겠다! 이렇게 되면 첫번째 뽑을 때의 경우의 수는 n이지만, 그 다음 뽑을 때는 앞에서 이미 하나를 뺐기 때문에 n-1개의 경우의 수가 나온다. 그 다음은? 역시 하나가 더 빠졌기 때문에 n-2개의 경우의 수가 나올 것이다.
이걸 k번까지 반복한다면

$\large n(n-1)...(n-k+1) = \frac{n!}{(n-k)!}$
전체 경우의 수는 이렇게 나오게 된다.
우리는 이걸 순열(permutation)이라 부르고, 팩토리얼을 사용해 나타낸다. 흔히 $_nP_k$로 나타낸다.

책에서는 n!을 근사하기 위한 스털링 공식에 대한 소개가 있는데, 그다지 필수적이지 않은 것 같으니 그냥 넘어가기로 한다. 

Sampling without Replacement and without Ordering 순서를 고려하지 않은 비복원 추출

이번에는 조합(combination)$_nC_k$을 보자. 순서를 고려하지 않고 뽑을 것이다. 이것을 순열과 연관시켜서 생각하는 방법이 있다. $_nP_k = \frac{n!}{(n-k)!}$ 이라는 것을 우리는 알고 있고, 이것은 순서가 고려된 값이라는 것을 또 알고 있다. 근데 k개를 순서짓는 방법이 몇가지 있을까? 첫자리에 k개의 경우가 들어가고, 그다음에는 이미 들어간 하나를 빼서 k-1개의 경우가 들어가고.. 하면 결국 k! 만큼의 경우의 수가 나온다. 그렇다면 우리는 이 k!만큼을 순열에서 나누어주면 순서를 고려하지 않은 순열, 즉 조합을 얻을 수 있는 것이다!

나중에도 보게 될 좋은 예시가 있다.
전체 n개의 공이 들어가있는 주머니에 k개는 흰 공이고, 나머지는 검은 공이다. 이 공들을 전부 한 줄로 나열할 때 나올 수 있는 모든 경우의 수를 구하라. 
흰 공끼리, 검은 공끼리는 서로 구분이 없기 때문에 나열되는 순서가 고려되어선 안 된다. 그러나 흰 공과 검은 공 끼리는 순서가 구분될 필요가 있다. 이 문제를 푸는 직관적인 방법 중 하나는, 일단 전부 검은색으로 칠한 n개의 공을 일렬로 나열하고, 그 중에 k개를 뽑아서 흰 색으로 칠하는 것이다. 이때 쓰이는 것이 바로 조합!

$\large \frac{n(n-1)...(n-k+1)}{k!} =\frac{n!}{(n-k)!k!} = \lgroup\frac{n}{k}\rgroup$
맨 끝쪽의 수식은 이항 계수(binomial coeffiecient)라 하여 n개에서 k개를 뽑는(choose) 경우를 나타낼 때 사용한다.

참고로 조합, 이항 계수는 이러한 특징을 지닌다. n개에서 k개를 뽑으나, n-k개를 뽑으나 경우의 수는 같다는 것이다. 어떻게 보면 n개에서 뽑힐 k개를 고르거나, 안 뽑힐 n-k개를 고르거나 하는 문제이기 때문에 꽤나 직관적이다. 
여기에서의 핵심은 k개를 기준으로 n을 분할한다는 데에 있다. 이 개념을 더 확장시킬 수 있는 방법이 있다!

위와 같이 전체를 분할하는 m개에 대해서 경우의 수를 저렇게 꺼낼 수 있다. 저 식을 다항 계수(multinomial coeffiecient)라고 부른다. 

Sampling with Replacement and without Ordering 순서를 고려하지 않은 복원 추출

마지막으로 순서를 고려하지 않는 복원 추출. 이거는 딱히 붙여진 이름은 없는 것 같다. 순서를 고려하지 않고 복원을 한다는 것은, k명의 사람들이 길거리 설문조사에서 n개의 선택지 중에 저마다 하나씩 스티커를 붙이는 행위와 같다. 이 예시는 내가 이전에 글에도 쓴 적이 있는 것 같은데, 이해는 가장 잘 되는 것 같다. 
책에서 나오는 예시도 비슷하다. n개로 분할된 공간에 k개를 분배하는 경우의 수를 구하면 된다.

뭐, 이런 식으로 나눌 수 있겠다. 그런데 여기에서 재밌는 지점이, '/' 이것을 하나의 대상으로 볼 수 있다는 것이다. 
현재 그림의 상태는 xx//x/xx인데, x와 / 모두 대상으로 본다면 이 문제는 아까 위에서 봤던 조합의 예시와 똑같은 문제가 된다. x를 검은 공, /를 흰 공이라고 생각해보자. 그러면 우리는 일단 검은 공을 쭉 나열한 뒤에 몇 개를 골라 흰 색으로 칠하는 문제와 똑같은 상황에 마주해있다.
그럼 /는 몇 개일까? n개로 분할된 공간이라 했으니 그 사이 구분선의 역할을 해주는 /는 n-1개가 있을 것이다.

그러니 n-1+k개에서 k개를 뽑는 상황이 바로 우리가 n개에서 순서를 고려하지 않고 k를 복원 추출하는 상황이라는 것이다. 

2.4 Conditional Probability 조건부 확률

여태 우리는 확률이 뭔지, 확률을 집합으로 표현하는 방법과 공리, 경우의 수를 셈하는 방법 등의 다양한 내용들을 다뤘다. 요컨대 확률 이야기를 하기에 앞서 필요한 것들을 이야기했다는 것. 이제는 조금 더 확률에 관해 알아보자. 

우리는 어떤 사건들을 이야기할 때, 두 사건이 어떤 관련성이 있음을 느낄 때가 있다. 가령 주사위를 한번 던져서 눈을 확인하는 랜덤 실험에서 짝수의 눈이 나오는 사건과, 5보다 작은 눈이 나오는 사건이 있다고 쳤을 때, 눈이 2 또는 4가 나오면 둘 다 두 사건 모두 일어났다고 볼 수 있을 것이다. 그러면 여기에서 짝수의 눈이 나오는 사건이 이미 일어난 상황에서 5보다 작은 눈이 나오는 사건은 어떤 확률을 가질지, 궁금해볼 법도 하지 않나!
두 사건이 서로의 발생에 있어 연관이 있는지를 볼 때 사용하는 것이 바로 이 조건부 확률(conditional probability)이라는 것이다. 

$\large P[A|B] = \frac{P[A\cap B]}{P[B]}$
B가 발생했을때 A가 일어날 확률은 이렇게 표시한다. 이때 B는 당연히 공사건이어서는 안 될 것이다.

왜 식이 이렇게 되는가? B가 발생한 상황이라 했으니 우리는 표본 공간을 좁혀서 생각할 수 있다. A의 입장에서, 가능한 모든 결과는 B가 일어난 상황 속에서 일어나는 것이기 때문이다. 그 상태에서의 A라는 사건은 B가 일어나지 않은 결과를 포함해서는 안 될 것이다. 그래서 둘의 교집합으로 분자를 나타내는 것이다.

상대도수 표현으로 먼저 이해하면 이해가 더 쉽다.
이러한 조건부 확률은 당연히 확률의 공리를 만족한다.

$\large P[A|B]P[B] = P[A \cap B] =P[B|A]P[A]$
또 한가지, 우리는 이 식에서 분모를 곱하여 이런 식으로 나타낼 수 있다. 이것에 의해 우리는 이후 다양한 개념들을 도출해낼 수 있다.

조건부확률이 연속된 랜덤 실험에서 어떤 식으로 활용되는가를 보기 위한 예시. 이런 식으로 구성된 그림을 우리는 트리 다이어그램이라고 부른다.
해당 예시를 설명하면 이렇다. 검은 공 2개와 흰 공 3개가 들어있는 주머니가 있고, 여기에서 복원하지 않고 두 공을 뽑는 실험을 한다. 여기에서 뽑은 두 공이 전부 검은색인 사건의 확률을 구해보자. 
복원이 없다는 것에서 알 수 있는 사실은 첫번째 공을 뽑는 행위에 의해 두번째 공을 뽑는 확률에 영향이 간다는 것이다. 그림의 트리 다이어그램은 그러한 확률을 나타내어주고 있다. $B_i$는 i번째에 검은 공을 뽑는 사건이다. 그러니까 우리가 구해야 하는 것은 $P[B_1 \cap B_2]$인 것이다. 그림의 확률을 본다면,

$\large P[B_1 \cap B_2] =  \frac{2}{5}\times \frac{1}{4} = \frac{1}{10}$
이고, 이는 
$\large P[B_1 \cap B_2] =  P[B_2|B_1]P[B_1]$
를 나타낸다.

현재의 예시는 연속된 랜덤 실험을 위해 이야기된 것이지만, 여기에서 꺼낼 수 있는 공식이 하나 있다. 따지자면 이건 위 아래로 길게 보는 것이 아니라 옆으로 넓게 보는 것이라고 할 수 있다.
만약 표본 공간을 분할(partition, 위에서 미리 말 안 했지만, 전체를 남김 없이 나눈다는 뜻이다)하면서 서로 배반인 $B_1, B_2 ... B_n$의 사건이 있을 때, 임의의 사건 $A$에 대해 다음이 성립한다.

직접 쓰기 심히 귀찮은 상태라 그냥 캡쳐.. 맨 마지막 식을 두고 전확률 공식(theorem on total probability)라고 한다. 
이것이 나타내는 것이 무엇인가? 전확률 공식은 한번에 알아내기에 지나치게 커서 알아내기 어려운 어떤 사건을 분할하여 접근할 수 있다는 것을 나타낸다. 우리나라 남자이면서 코로나 확진자인 사람의 확률을 알아내고 싶다고 했을 때, 이를 지역으로 분할하여 알아낸 다음에 그 확률들을 더해주는 것이 조금 더 편하다는 것!

위의 예시에 전확률공식을 사용하는 케이스를 보자. 두번째 공이 검은 공일 확률을 구하려면 어떻게 해야 할까?

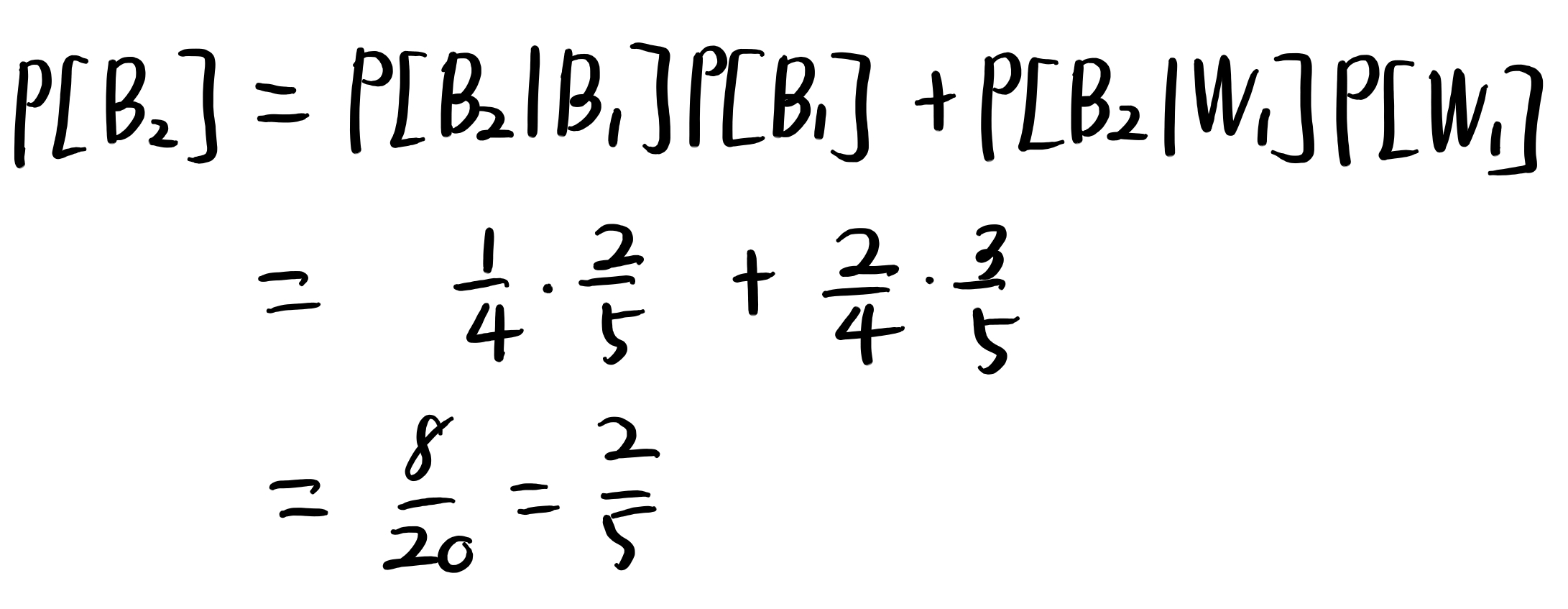
이런 식으로 알아낼 수 있는 것이다! 참고로 현재 나온 결과는 결국 5개 중에서 2개가 검은 공일 확률과 같다. 즉, 그냥 첫번째 뽑는 행위에서 검은 공을 뽑는 확률과 같다는 것이다. 이는 이전 확률이 현재 확률을 구하는데 있어 일절 의미를 가지지 않기 때문에 사실 꽤나 말이 되는 상황이다.

Bayes' Rule 베이즈 법칙

베이즈 법칙은 굉장히 유명하다. 그리고 사실 도출도 쉽다. 그런데 굉장히 유용하다! 머신러닝을 공부하는 사람이 베이즈 법칙을 모른다는 것은 정말 말이 안 될 것이다.

흔히 아는 가장 기본적인 형태. 이를 조금 더 일반화시킬 수 있다.

그게 바로 이것이다. B가 S의 분할인 상황에서 이러한 식이 성립한다. 분모가 전확률 공식을 통해서 쉽게 도출된다. 

보통 베이즈 법칙은 A가 발생한 기준으로 사전 확률(priori probability)과 사후 확률(posterior probability)를 나누고, 하나를 가지고 다른 하나를 구할 때 사용한다. 요지는 알기가 힘든 사후 확률을 이 공식을 통해 알아낼 수 있다는 것이다. 사전 확률은 대체로 구할 수 있는 경우가 많다. 그러나 사후 확률을 구할 때는 베이즈 법칙이 매우 유용하다.
이게 뭐 별 거인가 싶었는데, 나중 가면 이게 무궁무진하게 쓰인다는 것에 감탄을 금치 않을 수가 없었다..

2.5 Independence of Events 사건의 독립

조건부 확률을 여태 알아봤다. 그런데 B의 발생이 있어도 A의 확률이 변하지 않는 경우가 있을 수 있을 것이다. B가 발생하건 말건 상관 없이 A의 확률은 동일한 것. 이럴 때 우리는 A가 B와 독립적(independent)이라고 말하는 게 상당히 자연스러울 것이다.

아래 나온 식을 만족할 때 우리는 이제 독립이라고 말하면 된다. 이 정의에서 우리가 알아낼 수 있는 것은 A가 B에 독립이라면 B 역시 A에 독립이라는 것이다. 물론 어디까지나 각 사건이 공사건이어선 안 될 것이다. 결국 한 쪽이 다른 한 쪽에 영향을 주지 않는다면, 그것은 역도 성립한다는 것! 
독립은 무얼 뜻하는 걸까? 조건부 확률은 좁은 표본 공간을 새로 두는 것과 같다. 근데 독립이라는 것은 그렇게 새롭게 표본 공간을 두었음에도 해당 표본 공간에서의 사건은 같은 비율을 유지한다는 말이다.

재밌는 것은 서로 배반이면서 두 사건 모두 0보다 클 경우에는 독립이 절대 성립하지 않는다는 것이다. 위 식을 보면 알 수 있다. 배반이면서 독립이기 위해서는 A나 B 둘 중 하나가 공사건이어야만 식이 성립하게 된다. 반대로도 말할 수 있을 것이다. 두 사건이 독립이면서 공사건이 아니라면? 둘은 절대 배반이 아닐 것이다.

추가적으로 여러 개의 사건에 대한 독립을 알아보자. 정의해 의거하여 생각하면 여러 개의 사건의 교집합이 각 사건의 곱과 같으면 각 사건은 서로 독립이라고 할 수 있을 것이다.
간단하게 각 사건들이 독립이기 위해서는 모든 쌍을 고려해서 그 각각이 독립이 성립하면 될 것 같다. 그런데 여기에 추가적인 조건이 필요하다. 다른 사건들이 한꺼번에 일어났을 때도 각 사건의 독립이 성립해야 한다는 것이다.

위 예시를 보면 두 개의 쌍으로는 독립이 성립하지만 전체 독립은 성립하지 않는 것을 알 수 있다. 그래서 다른 사건들이 일어났을 때에 각 사건의 독립이 성립해야 한다는 것이다. 

이를 정리하면 이런 식이 성립한다. 이를 더 일반화하여 나타낸다면

이렇게 표현이 된다. 우리는 이것이 독립을 확인하기 위해 $2^n - n - 1$개의 경우에 대해 독립이 성립한다는 것을 보여야만 한다. 왜 이 정도의 경우의 수가 나오는가? 멱집합의 총 개수 $2^n$개에서 각 사건이 하나만 있는 경우 $n$, 그리고 공사건 하나를 빼서 이런 경우의 수가 나온다.
물론 보통은 이렇게 우리가 서로 독립인 걸 우리가 밝혀야 하는 상황이 거의 나오지 않는다. 대체로 우리가 접하는 확률 관련 문제에서는 이미 독립적인 실험들이 상황으로 주어질 것이다. 가령 동전을 여러 번 던지는 행위에서 각 부분 실험은 이미 독립이란 걸 이미 우리는 알고 있다는 것이다. 

책에서 나오지는 않는데 독립에 대해서 또 재밌는 성질이 있다.

독립인 사건들 간에는 무슨 짓을 해도 독립이라는 것.

간단하게 두 가지일 때 증명을 해보았다. 일반화시켜서 하는 것은 귀찮아서 패스..

이건 아까 서로 독립일 때의 상황에 대해 설명하면서 충분히 이해됐을 내용이다. 모든 경우의 수를 따져보라.

2.6 Sequential Experiments 순차 실험

원서로 읽다보니 번역본에서는 어떻게 번역되어있을지 궁금하다.. 아무튼 영어 표현에도 익숙해져보는 걸로. 방금 위에서 언급한 그런 실험, 동전을 여러 번 던지는 실험은 사실 자잘한 부분 실험으로 나뉘어져 있다. 동전을 한 번 던지는 실험이 모여서 하나의 실험을 이루고 있다는 것이다. 이런 식의 실험에 대해 조금 알아보자. 참고로 각 부분실험은 지금처럼 독립적인 경우도 있지만, 아닌 경우도 있다. 

Sequences of Independent Experiments 독립 실험의 순서열

sequence는 수학에서는 수열이라고 번역하기도 하는데, 이 개념이 수에 대해서만 성립하는 것이 아니다. 어떠한 배열인데 순서가 고려되는 배열, 그런 묶음을 나타낼 때 쓰는 표현인데 적절한 번역어가 떠오르지 않아서 순서열이라 이름짓겠다.

그래서 독립 실험의 순서열이 무어냐. 흔히 독립 시행이라 부르는데, 사실 별 거 아니다. 독립적인 부분 실험들인 상태에서 각 실험에서 일어난 사건의 교집합은 곱으로 나타낼 수 있다는 것. 방금 위에서 봤던 그 식을 그대로 적용할 수 있다는 것이다.

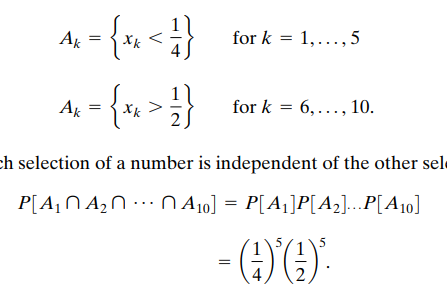
직관적인 예시라 가져온다. 초반 5개의 부분실험에서는 1/4의 확률로 성공이고, 이후 실험에서는 1/2의 확률로 성공인 실험을 할 때 모두 성공하는 확률은 저렇게 간단하게 곱으로 나타낸다.  

The Binomial Probability Law 이항 확률 법칙

방금 위에서 본 예시에서 조금 더 나아가보자. 위 사건은 순서가 고려되어 있다. 그러나 만약 순서가 고려되지 않는다면? 위 예시에서 $A_1$ 과 $A_2$에서 일어난 사건의 순서가 고려되지 않는다면 어떨까? {성공, 실패}, {실패, 성공}은 같은 것을 의미하는 실험이 있을 수 있다는 것이다. 

가장 간단한 실험은 동전 여러번 던지는 실험이다. 동전을 세번 던져서 나오는 앞면의 수를 기록하는 실험에서 {HHT}, {HTH}, {THH}는 앞면의 개수가 2라는 같은 결과를 내놓는다. 
나중에 더 보게되겠지만, 이렇게 앞면과 뒷면, 혹은 성공과 실패라는 오직 두 가지의 경우로 사건이 나뉘는 시행들에 대해서 베르누이 시행(Bernoulli trial)이라고 한다.

조금 일반화된 식을 한번 보자. n개의 독립적인 베르누이 시행에서 k개가 성공하는 확률은 이렇다.
여기에서 앞에 놓인 상수는 위에서 보았던 이항 정리이다. 
그리고 이러한 수식을 이항 확률 법칙(binomial probability law)라고 부른다.

이 식은 이항 정리(binomial theorem)를 나타내는 식인데, 이걸 통해 위의 수식을 증명할 수 있다. 간단하기에 생략.

점화식으로 나타내면 이렇게 되니 참고하자.

The Multinomial Probability Law 다항 확률 법칙

이항을 봤으니 이번에는 다항을 보자! 다항의 상황은 표본 공간을 분할하는 여러 개의 결과들이라고 말한 적이 있다.

그러한 상황에서 각 독립된 시행에서의 확률은 이렇게 상수로 다항 계수를 두는 식이 성립한다.

The Geometric Probability Law 기하 확률 법칙

나는 이게 왜 기하로 불리는지 잘 모르겠지만, 아무튼 확률론에서의 기하는 대체로 베르누이 시행을 하는데 처음으로 성공할 때까지 하는 시행을 하는 상황을 말한다. 동전을 던지는 시행을 하는데, 앞면이 나올 때까지 계속 던지는 것이다. 그리고 던진 횟수를 기록하는 실험일 때 이를 기하학적이라고 표현하는 듯하다.
개념 자체는 어렵지 않다. 앞면이 나올 때까지 던진다고 하면 동전을 m번 던졌다는 것은 무얼 뜻할까? 그전까지는 계속 실패했다는 뜻이다. 그러니까 m-1번 실패하고 마지막 한번을 성공한 상황이라는 것이다.

이런 식으로 확률 표현이 가능하다. 이렇게 확률을 부여하는 것을 기하 확률 법칙(geometric probability law)라고 부른다.

참고로 보다시피 기하 확률 법칙으로 부여된 확률은 다음과 같이 확률의 공리를 만족한다.

또한 재밌는 것이, 특정 횟수 이상의 확률을 구할 때는 이렇게 단순하게 실패할 확률을 특정 횟수 제곱을 해주면 된다! 동전을 던지는데 앞면이 나오면 성공이라고 해보자. 이때 3번 이상 던져서 성공을 할 확률은? 위 식에 따르면 간단하게 $P[X > 2]$라서 1/4이라는 것을 알 수 있다. 직관적으로도 알 수 있는 것이, 첫번째에 성공할 확률이 1/2 이고, 두번째에 성공할 확률이 1/4이니까 그것을 1에서 빼더라도 같은 값을 얻을 수 있다.

Sequences of Dependent Experiments 의존 실험의 순서열

독립 실험의 순서열에 대해 여태 실컷 알아봤으니 다음은 독립이 아닌, 의존(dependent) 실험의 차례. 여기에서는 체인처럼 맞물리는 상황을 생각해야 한다.

두 주머니에서 공을 하나만 꺼내어 기록한 후 다시 넣는 행위를 반복하는 실험을 한다. 주머니 0(이름이 0)에는 1이라고 적힌 공 2개와 0이라 적힌 공이 하나 있고, 주머니 1에는 5개의 1공과 1개의 0공이 있다. 처음에 어떤 주머니에서 공을 꺼낼지는 완전히 랜덤이다. 그 이후에는 꺼낸 공의 숫자를 확인하고 그 숫자에 해당하는 주머니의 공을 하나 꺼낸다.

이걸 격자 다이어그램(trellis diagram)이라 하여 여기에서 순서열을 구할 수 있다. 이 그림이 위의 예시를 나타내는 상황인데, 보기만 해도 복잡하다. 여기에서 핵심은 현재의 시행 확률은 바로 이전 시행 결과에 의해 영향을 받는다는 것이다.

그래서 이러한 상황을 생각할 수 있다. 딱 봐도 뭔가 연쇄 작용이 일어나는 것이 보인다.

이를 일반화하면 이렇게 표현할 수 있고, 이러한 것을 마르코브 체인(Markov chain)이라고 부른다. 또 이렇게 한 결과가 오직 이전의 결과에만 의존적일 때 마르코브 특성을 가진다고 말한다. 11장에서 더 자세히 다룬다고 한다! 
근데 지금의 예시는 직전에 의해서만 영향을 받는다고 하였기에 이렇게 단순화할 수 있는 거지, 그게 아니라면 이렇게 이쁘게 나오지는 않을 것이다..