20230107~8토~일-밑러닝32~37, 추천4지표 논문

이전 내용을 한 지 대충 3주가 되니 내용이 조금 가물가물하다. 복습하면서 대충 내용을 다시 다졌다.

우리는 고차 미분을 하고 싶다. 뉴턴 방법을 통해 최적화를 하면 효율적으로 학습이 이뤄질 수 있는데 이 방법은 2차 미분을 필요로 하기 때문이다. 그래서 우리는 우리 코드에 고차 미분이 가능하도록 적용할 것이다. 우리의 코드는 미분을 할 때 backward, 즉 역전파를 한다. 사실 역전파는 만들어진 계산 그래프를 거꾸로 올라가면서 이뤄지는 것인데, 달리 말하자면 역전파를 하면서 이뤄지는 계산 그래프에 대해 역전파를 할 수 있다면 n차 미분을 하는 것이 가능하다는 것이 된다. 그렇기에 backward 과정에 사용되는 값들을 변수 클래스에 담게 되면 자연스레 계산 그래프가 만들어질 것이고(계산 과정 상에서 알아서 변수 클래스가 함수 클래스를 인식하고 계산 그래프가 만들어지도록 되어 있다) 이를 통해 고차 미분이 가능하다.

밑러닝-32. 고차 미분(구현 편)

이제 진짜로 고차 미분을 코드로 구현해보자. 또한 이제부터는 이전에 했던 코드를 core_simple.py에 두었던 것과 달리 core.py에 수정을 가할 것이다. 이제 새로운 dezero로, 정말 최종적인 코드가 만들어진다는 뜻이다!

변수 클래스에서 생기는 변화. 해당 코드는 역전파를 처음 시작할 때 미분값 1을 직접 넣기 귀찮아서 짜여진 코드인데, 여기에서부터 미분값을 변수 클래스로 받는다. 이것만 해주면 이후에 이뤄지는 계산들은 변수 클래스와 함께 이뤄지기에 오버로드된 연산자들은 전부 함수 클래스가 될 것이고, 함수 클래스와 함께 이뤄지는 입출력은 전부 변수 클래스가 된다. 정말 간단하다!

구체적인 함수 클래스의 backward에서도 변화는 생기긴 한다. 원래는 들어온 변수 클래스의 데이터인 ndarray만을 받도록 되어 있었으나, 이제는 오가는 모든 변수들을 변수 클래스로 받기 위해 그냥 당당하게 self.inputs를 받게 된다. 
참고로 Add 함수는 단순하게 받은 값(ndarray든, 변수 클래스든)을 분기하여 그대로 돌려보내는 역할만 하므로 수정이 필요하지 않다.

이제 데이터를 꺼내받던 모든 구체적 함수들의 backward를 수정해준다.

추가적으로 변수 클래스에 create_graph라는 파라미터를 만들고 관리한다. with 문을 통해 일전에 역전파 계산을 하지 않도록 선택지를 만들었다. 그것을 여기에서 다시 사용하는 것. 고차 미분이 가능해졌다고는 하나, 항상 고차 미분을 하는 것은 아니기에 메모리를 절약하는 차원에서 이러한 조건을 걸어두는 것이다. 
이미 순선파는 이뤄졌기에 역전파 한 번을 하기 위한 계산 그래프는 만들어져 있는 상태. 이상태에서 역전파를 실행할 때 다음 역전파가 이뤄지지 않게 계산 그래프가 만들어지지 않도록 해주는 것이다.
주석이 달린 두 부분이 with문에 의해 영향이 간다.

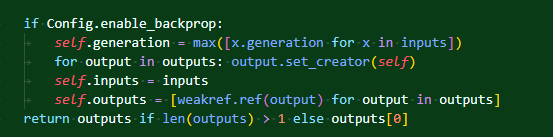
조금 더 복습을 해보자면 저 with문 내에서 실행될 때는 Config의 enable_backprop이 false가 되어있다. 그렇기에 함수와 변수간의 관계 형성이 이뤄지지 않는다. 이를 통해 불필요한 메모리가 사용되는 것이 방지된다.
no_grad를 쓸 수 없는 이유는 create_graph에 의해 역전파 비활성을 따지고 싶기 때문이다.
왜 create_graph의 기본값은 False인가? 실무에서는 역전파를 한번만 하는 경우가 많기 때문.

이제 core.py를 만들었으니 본격적으로 활용하자. 처음에 __init__파일을 만들었을 때는 simple core를 사용했지만, 이제는 정식 core를 사용하는 코드를 작성한다.

밑러닝-33. 뉴턴 방법으로 푸는 최적화(자동 계산)

이제 수정한 코드를 직접 사용해볼 시간이다.

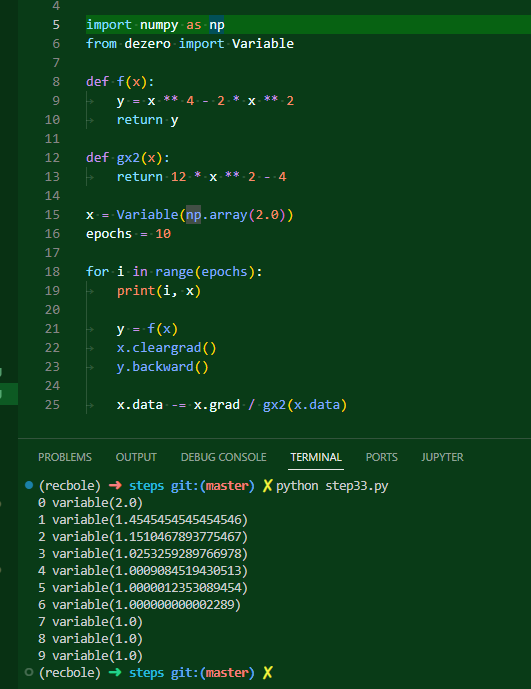
이것은 이전 29단계에서 수동으로 2차 미분을 계산하여 뉴턴 방법으로 최적화를 했었던 식이다. 7번 만에 최적화가 이뤄지는 것을 확인할 수 있다. 참고로 이 코드를 core파일로 돌리면 안 돌아간다.

처음에 안 돌아간 이유는 이러했다. 제곱 연산을 할 때 문제가 발생하더라는 것. 이건 어느 정도 어렵지 않게 해결할 수 있었던 것이, self.inputs는 리스트로 묶여있기 때문에 받을 때 그 리스트를 풀어주는 과정이 필요하더라고. 그래서 리스트니 뭐니 하면서 문제가 발생했던 것이었다.
나는 여기에 backward 부분에 create_graph만 만들어주면 해결될 것이라 생각했다.

그러나 다음으로는 이런 문제가 발생했다. 자세히 보니까 변수 클래스의 데이터에 변수 클래스가 들어가고 있는 모습이 확인됐다.

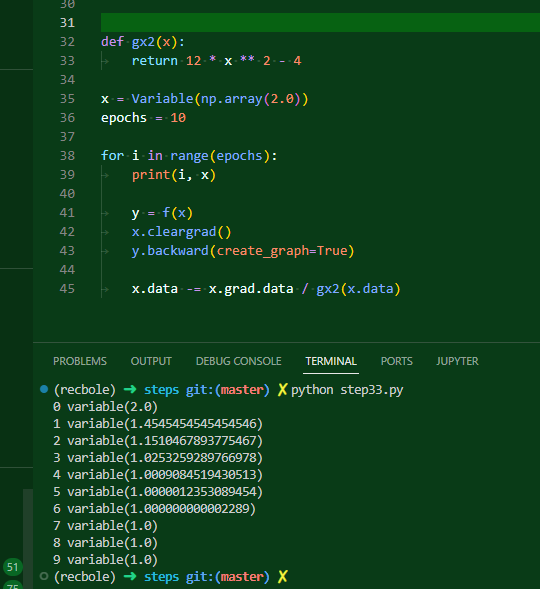
해결방법은 다음과 같다. 이제 x.grad는 명백히 변수 클래스이다. 그러니 안 속에 있는 데이터에 접근하기 위해서는 x.grad.data로 접근하는 것이 옳다. 이전에는 그렇게 하지 않았기에 계산 과정 상에서 x.data에 계산이 된 변수 클래스가 들어가는 상황이 발생했던 것이다.
뭐.. 아무튼 이전 코드를 현재 수정된 사항에 맞춰서 고쳐쓰면 이렇게 고쳐쓸 수 있다는 뜻일 뿐이다. 우리는 구태여 2차 미분된 도함수를 직접 만들어서 쓸 필요가 없다!

이제는 당당하게 고차미분해서 쓸 수 있다~ 이 말이다. 참고로 미분을 진행할 때마다 +연산에 의해 미분값이 중첩되기에 중간에 꼭 clreargrad를 해줘야만 한다. 그리고 각 역전파를 통한 값을 변수로 저장해서 업데이트를 해주면 끝! 
우리 코드가 고차 미분을 잘 행하고 있다는 것을 확인할 수 있다.

밑러닝-34. sin 함수 고차 미분

현재 본격적으로 우리의 코드를 라이브러리화를 진행하면서 연산자 오버로딩이 가능한 하위 함수들만 구현을 했었다. 그럼 이제 다른 함수도 슬슬 구현해보자. 먼저 sin 함수!
우리는 일찍히 27단계에서 sin함수를 구현한 적이 있다.

테일러 급수를 통해서 sin함수를 나타내보겠답시고 했던.. 그 시절에 테스트용 sin 함수를 구현할 때의 모습은 이러했다.

연산자 오버로딩을 하지 않은 모든 함수들은 이제부터 funtions 파일에 넣는다! 이전 코드와 비슷하게 만든 방식인데, 이렇게 하면 

이런 문제가 발생한다. x는 변수 클래스라 넘파이의 함수에 들어갈 수 없기에 발생하는 문제이다. 그렇다면 여기에도 np.cos(x.data)라는 식으로 할 수 있지 않을까? 생각했는데, 그러면 이후부터 grad가 none이 되어서 고차 미분이 진행되지 못한다. 정확하게 왜 그렇게 되는지는 파악이 안 됐다.

이렇게 애초에 전부다 변수 클래스 활용하여 함수를 짜면 아무런 문제가 없다.

 sin함수를 3번 더 미분해 들어간 값을 전부 그림으로 나타냈다.

밑러닝-35. 고차 미분 계산 그래프

이번에도 새로운 함수를 추가해보자. 이번에 추가할 것은 하이퍼볼릭 탄젠트! 쌍곡탄젠트라고도 불린다. -1, 1 사이의 값을 내뱉으며 시그모이드의 단점을 보완했다는 평가를 받기도 한다고 한다. 
왜냐? 중앙값이 일단 0이니까 좀 깔끔하다. 그리고 미분 최댓값이 1까지 나온다. 시그모이드는 0.3까지 나오는데.. 그래서 기울기 소실에서 조금 더 자유롭다고 한다. 
그러나 시그모이드는 0과 1사이의 값을 내기 위해서 쓰는 것이라면, 퍼센티지를 나타내기 위해 쓰는 것이라면 당연히 대체될 수는 없을 것으로 생각된다.

$\Large y = tanh(x) = \frac{e^x - e^{-x}}{e^x + e^{-x}}$

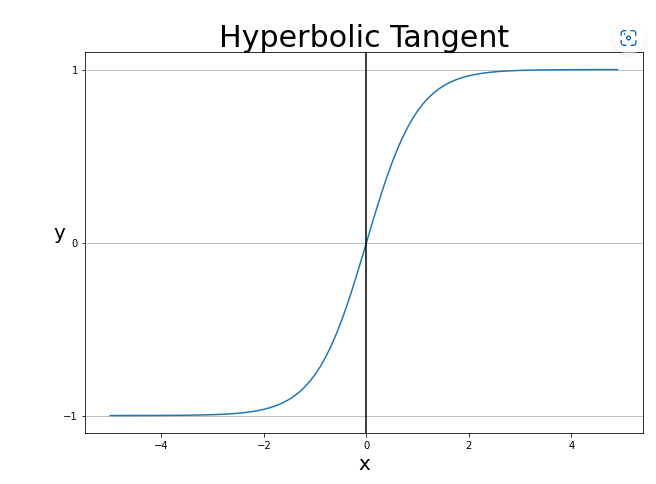
대충 요래 생긴 함수. 기억 상으로는 이 놈도 활성함수로 많이 쓰였다는 것 같다.

이 놈은 미분하면 $1 - y^2$라는 간단한 식이 튀어나온다.

대충 이러한 식으로 쌍곡탄젠트의 계산그래프를 그릴 수 있다. iters 를 조절하면 아주 드라마틱한 그림이 나오게 된다. 근데 서버에서 돌리려고 하니 dot이 안 깔려있다고 하는데 귀찮아서 구태여 깔지는 않았다.. 대신 깃헙에 올라와 있는 그림을 보자면, 

이 그림이 8차 미분을 했을 때의 그림이다.

중간을 확대시켜보면 이런 모양을 하고 있다. 처음에 이 책을 둘러볼 때 이 사진이 나온 페이지를 보고 깜짝 놀랐던 기억이 있는데 결국 내가 이쪽 단계까지 왔다!

밑러닝-36. 고차 미분 이외의 용도

고차 미분 자동화 구현의 요지는 역전파 시에 연결이 이뤄지도록 하는 것이다. 이를 통해 역전파 위에 역전파를 하는 식으로 중첩이 가능하다. 이를 흔히 double backpropagation이라고 부른다고 한다. n번 할 수 있지만, 두 번 할 수 있다는데에 주안점을 둔 표현인 듯.

굳이 위에서 본 것처럼만 활용할 수 있는 것은 아니다. 이 코드를 보면 gx에 바로 연산을 하여 z를 만드는 모습을 볼 수 있다. gx는 단순히 계산된 수치가 아니라 계산 그래프가 형성된 상태의 값이다. 그래서 z를 역전파하고 나면 x의 미분값에 변화가 생기게 된다.

아무튼, 용도는 무궁무진하다는 것! 고차 미분의 방식은 많이 쓸 일은 없다고 한다. 이걸로 3고지, 고차 미분 계산은 끝이 났다. 4고지부터는 본격적으로 신경망용으로 우리의 프레임워크를 활용하고 개선할 것이다.

밑러닝-칼럼: 뉴턴 방법과 double backprop 보충 학습

그전에, 제 3고지의 칼럼을 보자. 내용이 꽤 어려워보인다.

여태 우리는 입력이 스칼라로 들어오는 경우를 많이 따졌다. 그런데 벡터나 행렬로 들어오는 경우도 있을 수 있다. 앞으로는 많이 따지게 될 것이기도 하다.

자코비안(Jacobian) 행렬의 기하학적 의미 - 공돌이의 수학정리노트 (angeloyeo.github.io)

너무 어렵다.. 간략하게라도 개념 이해를 하고 넘어가고 싶은데

음. 일단 헤세 행렬부터 보자고. 간단하게 말하자면 한번 편미분이 된 벡터에 대해 한번 더 미분을 진행한 행렬을 말하는 듯하다. f가 연속이라면 대칭 행렬이라고 한다. 만드는 방법은 미분된 상태의 식에다가 그대로 한번더 미분을 진행하면 나오는 듯.
다변수 함수가 있다고 쳐보자. $f(x_1, x_2, x_3 ..x_n)$ 이런 모양인 것이다. 여기에 전부 편미분을 하면 그라디언트 벡터가 나온다. 그리고 거기에다가 또 전부 편미분을 해주면 되는 것이다.

가우스-뉴턴 법이라고도 부르는 모양이다. 연립방정식의 근사해 구하기. 연립방정식은 전형적인 다변수함수들이다.
대충 봤을 때는, 그라디언트 벡터가 층층이 있으면 야코비 행렬인 것 같다.

다크 프로그래머 :: 뉴턴법/뉴턴-랩슨법의 이해와 활용(Newton's method) (tistory.com) 이 글의 도움을 최대한 받았다. 아직도 완벽히는 정리가 안 된다. 그래도 대충 아이디어는 알 것 같다.

책에서 나온 다변수함수, 벡터가 변수로 들어가는 함수에 대한 뉴턴 방법이 왜 저런 모양이 나오는지 이제야 알았다. 도중에 나오는 야코비 행렬, 헤세 행렬이 무엇인지도 얼추 알게 되었다.

요컨대 연립 방정식(벡터 함수라고도 표현되는 듯)에서 편미분한 도함수들의 행렬이 바로 야코비 행렬이다. 그라디언트 벡터들의 모임인 격. 아직 개념은 확실치 않지만, 다음 장에 나오는 내용으로 보아 하나의 그라디언트 벡터도 야코비 행렬이라고 보는 것 같다. 결국 벡터도 1 x n 모양의 행렬이라고 할 수 있으니까.
헤세 행렬은 그러한 그라디언트 벡터 하나를 다시 편미분한 행렬이다. 2계 도함수로 만들어진 행렬이라고 정의내려지는 듯하다.

이정도 이해면 얼추 맘 편히 넘어갈 수 있을 것 같다. 근데 헤세 행렬은 항상 역행렬을 가지는 것일까? 사실 아니더라도 이전에 역행렬의 역할을 대신 해주는 행렬에 대해서 배운 적 있는 것 같기도 하다.

아무튼 뉴턴 방법은 참 좋은데, 뭐라 설명할 방법도 있는데, 좀처럼 이쪽 업계에서는 잘 안 쓰인다. 왜냐하면 변수가 많아질수록 헤세 행렬의 크기가 커지기 때문이다. n개의 매개변수면 헤세 행렬은 무조건 제곱을 취하기 때문에 n * n의 행렬을 만들어야 한다. 그만큼의 메모리가 사용되고, 또 역행렬 계산에는 세제곱 만큼의 메모리가 필요하게 된다고 한다. 
신경망에서는 매개변수가 100만 개를 넘어가는 일이 허다하니 현실적으로 뉴턴 방법을 그냥 적용하는 게 불가능한 것이다.

이를 보완하는 방법들이 있다. 이름하야 준 뉴턴 방법Quasi-Newton Method. 헤세 행렬의 역행렬을 근사해서 그 비용을 줄여보고자 하는 것이다. 대표적으로 L-BFGS가 있다. 이것은 기울기만으로 헤세 행렬을 근사한다.
근사값을 활용해여 계산 비용과 메모리를 절약할 수 있다는데, 여태까지 딥러닝에서는 기울기만을 이용하는 최적화 방법이 대세를 이뤄서 잘 쓰이지는 않는다고 한다. 
왜 그럴까? 메리트가 없는 걸까?
machine learning - The reason of superiority of Limited-memory BFGS over ADAM solver - Cross Validated (stackexchange.com) 
이 글을 보니 작은 데이터셋에서 adam보다 효과적이었다고 나와있다. 대충 읽어봤을 때는 아무리 그래도 큰 규모로 넘어가면 뉴턴 기반이 힘을 못 쓴다는 것 같다. 근사하는 것의 한계인 걸까, 비용 소모가 큰 걸까.

아무튼, double backprop은 헤세 행렬과 벡터의 곱에서 쓰일 수 있다. 해당 행렬 자체가 필요한 게 아니라 그 곱의 결과만 필요할 때 아주 요긴하다!

fx라는 행렬과 v라는 벡터가 있다. 이때 이러한 식이 성립한다고 한다. 이것에 대한 증명까지는 아니지만 이것이 맞다는 것은 책에 나와있으니 나는 그냥 넘어가련다. 이때 좌측식은 방금까지 봤던 헤세 행렬과 벡터의 곱이다. 
그렇지만 우측식은 벡터 간의 내적 이후 기울기를 구하라는 말과 같다. 그래서 행렬을 만들 필요가 없어지고 계산 효율이 올라간다. 그리고 이 우측식은? backward가 두 번 돼야 계산될 수 있다!

밑러닝-37. 텐서를 다루다

이제는 4고지, 신경망을 다루는 단계까지 왔다. 대체로 머신러닝에서는 텐서를 다룬다. 이번 고지에서는 본격적으로 그러한 적용을 할 것이다. 그 첫번째로! 텐서를 다뤄보자. 

라고는 하지만 사실 우리는 ndarray에 데이터를 담아 사용해왔기 때문에 넘파이의 기능의 덕을 볼 수 있다. 넘파이는 알아서 원소별 연산과 브로드캐스팅을 해주니까!

책 예제에서는 뒤에 나올 sum 함수를 미리 구현하여 우리의 dezero가 어디에서는 잘 작동한다는 것을 보인다. 최종 출력이 스칼라로 나오고 입력은 텐서로 들어가는 흔한 머신러닝에서의 방식에 대해, 우리가 여태 만들어둔 코드는 잘 작동하도록 되어있다.
여기에서 또 알아야 할 특징은 순전파와 역전파의 데이터의 형상이 일치한다는 것이다. (2,3)이 들어간 변수는 그 미분값 역시 (2,3)의 모양을 하고 있다(책에서 앞으로 미분이라 안 하고 기울기라 하겠다고 못을 박았으니 나도 그리 해야겠다.).

아무튼 이번 단계의 내용은 텐서를 우리가 이미 다룰 준비가 되어 있다는 것 정도가 되겠다.
여기에서도 부록 격의 내용이 나온다. 텐서에서 역전파가 어떻게 이뤄지는지를 따지는 것이다.
텐서가 들어가서 텐서가 나오는 식은 야코비 행렬을 통해 입출력의 미분을 따질 수 있다. 
이것이 쓰이는 지점은 바로 합성함수의 경우이다. 최종값이 스칼라인 경우를 따져보자. 
이때 연쇄법칙을 전개하면 중간의 미분값이 행렬의 형태를 띄게 된다. 이때 자동 미분을 앞에서 할지, 뒤에서 할지의 차이가 나오는데 뒤에서부터 할 경우 최종값인 스칼라에 대한 미분은 벡터로 나오기에 이후 계산도 지속적으로 벡터를 단위로 이뤄지게 된다. 앞에서부터 하게 되면 행렬을 계속 계산해야 한다. 자세한 내용은 책 참조!
이전에 자동 미분이 왜 항상 거꾸로 돼야 하는가에 대한 물음이 있었는데 이러한 이유가 있었다. 머신러닝에서는 대부분 최종값이 스칼라나 작은 차원의 벡터로 나오게 되고, 이쪽에서부터 출발하는 것이 계산에 있어서 훨씬 유리하다.

렉볼 SASRec

우리 팀은 일단 종류 별로 다양한 모델을 활용해 시각화를 이뤄낼 방법을 구상하고 있다. 나는 이중에서 SASRec을 맡았고, 원래 생각은 베이스라인 코드를 통해 모델을 구현하는 것이었으나 전반적으로 팀이 렉볼을 사용하는 것으로 방향을 잡았다. 그래서 나도 내친 김에 렉볼 시계열 모델에서 중복 추천하는 문제를 해결하는 방법이나 모색해보려고 한다.

sasrec은 두가지 로스가 주어진다. 영화 베이스라인에서는 따지자면 bpr이었을 것이다. 코드로도 한번 확인해보자. 
모델 단에서는 확인할 수가 없다. 아무래도 trainer에서 로스를 따지는 부분으로 가야할 것 같다.

우리가 사용할 데이터는 ml-1m이다. 이거 사용한다고 설정만 해도 이놈들이 알아서 다운을 받아주는 모양이다.

렉볼의 전체적인 것들을 다시 공부해보자. LS로 건드리면 무조건 leave_one_out 쪽으로 가게 되는 것이었던 모양이다. 그럼 여태 내가 의도한 대로 코드가 작동하지 않았다는 것이다. 일전에 내가 딱 한번 렉볼 내 코드를 수정한 적이 있는데, 의미가 달랐기 때문에 그때 그 코드가 그렇게 작동했던 것으로 보인다. 흠. 그러면 그거대로 조금은 난처하다. 

다시 논문

4가지 지표 부분은 다 읽어서 정리만 하고 본격적으로 아이디어를 구상해볼 예정이다. 그전에 남은 부분을 조금 읽으면서 내가 또 알아야 할 부분들을 정리해나가봐야겠다.

문서 파파고에 넣을 때 줄바꿈이 계속 들어가는 게 짜장나서 방법을 찾다가, 그냥 vs코드에 옮기고 한 줄로 만들면 되지 않을까 하는 생각이 들었다. 그냥 이러고 한 줄로 만들어버리면 끝 아닌가? 

\[[\w .;]+\] 내친 김에 정규표현식 공부도 조금 해서 조금 더 편리하게 전처리를 할 수 있도록 했다. 정규표현식도 제대로 공부하고 쓰는 시간을 가져야 조금 적응을 할 것 같은데 필요할 때만 잠깐잠깐 보다보니 계속 기억이 휘발된다...

정확성 외 지표에 대해 유저의 인식 측정하기

오프라인 평가를 통해 이러한 지표를 계산하곤 한다. 엄밀히는 사용자의 피드백이 필수라고 할 수 있겠다. 피드백에 대해 판단 편향이 생길 수도 있고, 비용 발생의 이유. 또 영화 같이 소비 시간이 긴 아이템에 대해서는 유저가 모르는 아이템에 대해 관련성, 다양성, 의외성 등의 판단하기 어렵다.
이 섹션에서는 사용자에 의존하는 작업들을 알아본다. 내가 볼 필요는 없다는 뜻이다.
하지만 우리 프로젝트의 주제에 대해서 이야기할 때 오프라인과 온라인의 부조화에 대한 이야기가 있었으므로 해당 내용이 관련이 될 수도 있다는 사실은 알아두는 게 좋겠다.
연구에서 다양성을 느끼게 하는데 있어서 관련성이 적은 아이템끼리 가까이 해서 추천을 하는 게 좋다고 함. 사용자는 이해되는 추천에 대해 확신을 얻는다. 다양성이 무조건 좋기만 한 것은 아닐 수도.
음악 추천에서 의외성을 최적화하는 추천이 의미가 있었다고 한다. 새롭고 흥미로운 아티스트를 추천하더라는 것.  어느 정도의 정확성을 희생하고 이걸 높이는 게 의미가 있다.
실질적인 a/b 테스트는 부족하다고 한다.

오프라인에서의 분석

각 지표는 어느 정도 서로 영향을 미친다. 한 지표에 대한 최적화가 다른 지표에도 영향을 줄 수 있다. 
이전 연구들을 먼저 살펴본다.
어느 데이터셋에든 각 지표에 좋은 모델이 달랐고, 결과도 달랐다. 통상적으로는 앙상블한 것이 결과가 좋았댄다.
knn에서 k가 커질수록 참신함이 줄어든다. 유저 기반은 아이템보다는 참신하다. 유저기반이 더 다양한 추천. k가 커지면 줄어들지만, 그래도 유저 기반이 더 다양하고 참신하다.
무비렌즈에 대해, knn과 암묵적 피드백(bpr인듯), 아이템 기반 추천. 정확성을 높일수록 참신성이 떨어진다. 커버력에 대해서는 bpr이 컨텐츠 기반보다 좋았다.
의외성은 다루는 게 적다. 커버력과 의외성은 높은 상관관계를 가진다. 나머지와는 별로.

재밌는 접근 방식은 이미 만들어진 것에 순위 재정렬하는 것. 아니면 처음부터 정확성 이외 지표 최적화하는 모델 새로 만들거나.
트레이드오프를 명시적으로 제어하려면 순위 조정 접근법이 좋다! 그러니 순위 조정 하는 방식으로하자. 
이게 뭐냐? 이미 학습돼서 추천된 리스트가 있으면 그것을 재정렬해서 추천하는 방식.

이거 쓰자. 관련성, 그리고 위의 다른 지표들을 나타내는 obj가 결합한다. 실험에서는 일단 알파는 0.5로 뒀다고 한다.

다양성 재정렬

다양성 식은 거리재서 하는 방식. 이때 거리는 아이템 피쳐, 그리고 평점 기반 둘 다해봤댄다. 평점 비슷하면 거리 가깝게 하고, 피쳐는 아마 자카드같은 거 쓰지 않았을까.

혹시나 했는데 역시나.. 만만한게 자카드지. 자카드가 높으면 비슷하다는 거니까 다양성점수가 떨어진다. 그래서 1에서 뺀다. 장르로 영화에 대해 거리를 따질 수 있는데, 무히려 장르로 작가도 따질 수 있는 모양이다. 어떻게? 작가가 만든 영화의 장르 집합을 만드나?

평점 관련 거리는 이렇게. 0과 1사이로 정규화된 상태의 코사인 유사도. 하이바가 있는 것은 해당 아이템의 평점 평균이다. 
두 아이템에 대해 모두 평점을 내린 유저에 대해서만 계산이 이뤄진다.

의외성(놀라움)

유저가 여태 본 아이템과 다른 아이템이면 놀라울 거다. 특정 아이템과 유저 프로필사이에서 최소 거리를 따져서 그 다른 정도를 따진다. 유저 프로필 전체의 평균 지점에서 따지지 않는다. 정보 손실이 있을 수 있어서 그렇다.
두가지 거리함수를 통해 놀라운에 대한 정의. 하나는 한 유저가 아이템 쌍을 볼 가능성을 측정하기 위해 평점을 사용한다. 이건 어느 정도의 근사치는 제공한다. 다른 하나는 컨텐츠 기반으로 거리를 잰다.
여기에서는 관련성을 고려하지 않는다. 그리고 순위도 인식하지 않는다고 한다. 여기에서의 순위는 추천 리스트 내의 순위.

첫 정의. 해당 아이템이 유저 프로필의 아이템과 같이 봐질 확률. 이건 쌍별 문제. 그래서 정규화된 pmi(상호의존정보) 지표를 쓴다. 두 아이템의 상호 의존성을 측정하는 것이라고 한다.

손으로 쓰기 매우 귀찮다! 아무튼 pi는 전체 유저 중  해당 아이템과 상호작용한 유저 수인 듯. 오른쪽은 두 아이템과 상호작용한 유저 비율. 값이 -1부터 1까지 나온다. -1이면 음의 상관, 0은 독립, 1은 양의 상관. 양이라면 유저입장에서는  덜 놀랍겠지?
이 공식을 가지고 아이템 i에 대해 해당 유저의 놀라움을 측정한다. 유저의 프로필 아이템에 다 써보는 거지. 이걸 0과 1사이로 정규화한다.

분수가 나오는 게 바로 정규화하는 것. min 때리는 게 유저와의 최소 거리를 따지는 거다. 유저가 호러, 판타지 영화를 봤다 치면 스릴러라는 아이템은 호러랑 그나마 좀 가까울 거다. 그 걸로 유저에게 느껴질 놀라움을 따지겠다는 것.
R이 등장하지 않는다. 즉 이미 추천된 리스트하고는 관련이 없다는 것이다. 이 지표는. 관련성 안 따진다느게 이건가?
일단 이 pmi는 유저가 본 걸로 따진다. 유저의 상호작용 정보를 통해 상호의존성을 파악한다는 거다. 이게 좋은 방법인지 함 이야기 들어보면 좋을 듯.
그리고 최소로 따지는 게 정말 좋은가도 따져야하지 않을까 싶기도 하다. 유저가 완전 판타지 러버인데 어쩌다 한번 호러 한번 본거라면, 스릴러를 추천하면 많이 놀라울 수도 잇다.
지표를 다양하게 표현하는 것이 얼마나 좋은 것일까?

이건 컨텐츠 활용해서 놀라움 따지기. 유저 프로필 내 아이템들과 비교. 자카드로 잰다. 그때 가장 작은 값으로 따진다.

참신성

참신성은 인기도와 관련되는 지표였다. 이 식은 해당 아이템과 상호작용한 유저 비율로 정보량을 표현하는 것이다.
이건 이전 식과 확실히 다르게 느껴진다. 엄밀히 크게 다르지는 않네. 이걸 평균내면 이전 식이구나. 인기도는 간단하게 이렇게 표현할 수 있다는 것이다.

이것들로 순위 재정렬을 할수 있다.

본격 실험

이렇게 지표 준비하고, 일단 재정렬하기로 했으니 넉넉하게 50개 뽑았댄다. 그 상태에서 10개 추천을 했다고 한다.
여태까지 정밀도를 지향하며 적게 추천을했다. 최상단만 추천하겟단 거지. 이 글에서는 1+랜덤 방법론을 가져온다. 
1000개에 대해서 평점 예측을 수행하게 한다. 근데 이때 유저가 최고로 추천한 거 하나를 여기에 추가해서 1001개를 에측하게 하고, top k에 그 하나가 들어가는지 보는 거다. 들어가면 히트다 히트. 그리고 이 히트 비율을 recall이라 부른다.
그러니까 이미 평점이 있는 데이터를 뺏다는 거네. 
이건 꽤 재밌는 방법으로 보이긴 한다. 우리 아이디어와 비슷한 게 있다. 우리는 오답지에 대해서 생각했떤 건데, 아무튼 비슷한 방식인 듯하다.
근데 이 가정은 그 하나가 다른 1000개보다 높다고 가정하고 있어 위험하다. 킹치만! 그 1000개가 전부 유저가 본 아이템을 기반으로 하지 않는다면 이야기가 충분히 이 가정이 의미가 있으 수 있다고 논문은 말한다.
음 이 1000개는 유저가 평점을 줬을 수도 있고 아닐 수도 있고? 그럼 정확성 자체는 유저가 실제로 본 비율? 갑자기 드는 생각인데, 이런 추천 테스크에서 recall과 acc는 그냥 같은 값을 나타내는가?

뭐, 일단 리콜이랑 커버력은 재정렬 접근에 대해 상응하지 않는다. 그러니까 우리는 recall, coverage, diversity(jaccard), diversity(cosine), serendipity(pmi), serendipity(jaccard), novety 해서 7개의 지표를 가지게 되는 것이다.

데이터는 무비렌즈 우리가 쓰는 것과, last.fm 1k 짜리를 썼다고 한다. 이건 우리한테 그다지 중요한 사항은 아니다. 우리가 이 논문을 재현할 것이 아니니까.
암튼 영화당 평균 1.65의 장르가 있다한다. 여기에 imdb를 또 따로 불러왔다는데; 뭔가 또 이상한 피쳐를 가져온듯. 이걸로 영화당 60개의 라벨을 만들었댄다.
last.fm 데이터 희소하답시고 지네 맘대로 잘라버린다. 그래도 되는거냐..? 흠. 생각해보면 안 될 건 없다. 근데 그렇게 잘라내놓고 뻔뻔하게 커버력이랑 참신성을 재냐..?

• a pairwise learning-to-rank algorithm(LTR)
• a PureSVD matrix factorization algorithm implemented using the sparsesvd library8 (MF)
• a user-based collaborative filtering method (UB)
• an item-based collaborative filtering method (IB)

이렇게 4개의 모델을 사용했다고 한다.

에잉 귀찬.. 이런 거 튜닝해줬댄다.

그래서 이렇게 선택했댄다.

이를 통해 본 것은?

1. 일단 리콜을 최적화 지표로 삼은 각 4개의 모델의 각 지표들 비교.
2. 그리고 이걸로 순위 재정렬!

일단 1번부터. 무비렌즈만 보자 귀찮으니까! 일단 ltr, mf가 성능이 좋았다. 그리고 다양성에서도 좋음. ltr은 참신성과 커버력에서는 mf를 한참 이긴다. 이는 mf 알고리즘이 인기도 기반으로 한다는 것을 나타낸다(..!).  knn이 의외성에서는 이긴다.
다른 연구에서는 커버력이 좋은데 참신성이 구질했다고 이야기하는 곳도 있다. 근데 여기에서는 커버력과 참신성의 상관관계를 보일 수 있었다!고 이야기하는중. 
knn은 아이템이든 유저든 다 비스무리. 근데 커버력에서는 유저랑 아이템이 차이가 심하다. 아이템 기반이 커버력이 좋네..
애초에 실험환경이 다른 것 같은데 뭘 자꾸 다른 논문을 들먹이는지.
k를 어떻게 정하냐에 따라 knn은 지표 값이 많이 변화한다고 한다.

이제 2번. mf 한 모델에 대해서 베이스라인(모델간 비교 그래프에 나온 그 추천 결과)과 각 지표를 토대로 재정렬 했을 때의 각 지표들을 나타냈다.
당연하지만, 각 그래프는 각 지표로 재정렬을 하다보니 해당 지표의 값이 높아진 모습을 볼 수 있다.
그리고 위에서 봤듯이 recall과 커버력은 그냥 하나의 값으로 나온다. 그래서 범위가 따로 없다. 다른 놈들은 추천 리스트의 아이템마다 값이 있기 때문에 그것을 평균내서 막대로 나타내고, 그 범위를 표시해뒀다.

 

 

회고 및 다짐

토

이번에도 할 일이 많구만. 스터디를 할 때 도무지 대충 할 수가 없다. 어느 정도만 이해됐으면 넘어가도 좋으련만, 내용이 정말 기초적이라고 판단이 되니까 대충 넘어갔다가 이후 내용에서 흐름을 놓칠 것이 우려되기도 하고 내 기반을 닦는데 있어서 확실하게 도움이 될 것 같아서 선뜻 어련히 하질 못하겠다. 결국 하루를 매번 다 투자하는 꼴이 나오는데 이게 참 애매하네. 최종 프로젝트에 영향이 없을 것이라고 확신을 못하겠다. 또 적당한 타협점을 찾기는 해야 한다. 

그래서, 렉볼을 어떻게 할 지도 관심사항이다. 아무래도 새롭게 베이스라인을 짤 필요가 있을 것 같은데 일단 각자 잡고 있는 판국이라 확실하게 통합하는 시기가 필요할 것으로 생각된다. 수헌이 형이 잡고 있는 것 같으니 나는 내가 짠 코드를 토대로 하는 정도에서 그치는 게 좋을 것 같다. 마침 안 그래도 시계열에는 아주 중요한 문제가 남아있다. is_sequantial이 True라 중복 추천이 되는 문제이다.

지표에 대한 이해도를 높이는 것이 일단 더 중요하다고 생각하는데, 아무래도 시간 상 당장은 무리인 것 같다.

그러고보니 짧은 기록. 생기는 고민이나 질문사항이 계속 제대로 업데이트가 안 되는 것 같아서 그냥 내가 만들어봤다.

일

머리가 왜 이리 아픈지. 감기가 이렇게 오래 가는 건 처음이다. 막 아프지는 않은데, 머리가 계속 띵하다. 목도 안 아프고 코도 안 나와서 다 나았나 싶었는데 조금 찬바람 맞아서 그런가?  휴식이란 게 뭘까? 무엇이 몸을 위한 휴식일까? 그냥 누워있는 것? 그러면 누워서 공부하면 몸은 휴식하고 머리는 공부할 수 있는 건가? 
..? 시도해볼까? 그러다 자면 어쩔 수 없는 거라치고, 일단 몸 건강에 최적화를 시켜야지.