20221217~8토일-밑러닝, 라이트닝, 리트코드
저번 주에 나갔던 내용이지만 글로 적지는 못 했던 것들. 글로도 적어놔야 나중에 다시 보기 편할 것 같아서 남겨두려고 한다.
밑러닝-20. 연산자 오버로드(1)
변수 객체에 일반적인 연산자를 쓸 수 있도록 바꿔보자! 간단한 연산자로 특정 동작을 덮어씌운다 하여 연산자 오버로드라고 부른다. 이제부터는 +, * 같은 기호를 변수 객체에 바로 쓸 수 있도록 만들 것이다.

일단 간단하게 곱셈을 하는 함수부터 만든다. 역전파 과정은 간단하다. xy일 때 x에 대해 미분하면 y가 상수 취급하여 y가 남고, 반대도 같은 방식이다.


우리가 할 일은 곱하기나 더하기 같은 것을 이렇게 귀찮게 표현하지 않고 오른쪽의 우리가 흔히 쓰는 기호로 표현하는 일이다. 객체 속에 특수 메소드를 이용해 사용자 지정 함수가 도출되도록 만들어 주는 것이다.


이를 위한 방법은 두 가지가 있다. 왼쪽처럼 변수 객체 안에서 직접적으로 해당 메소드를 만들어주거나, 객체 바깥에서 해당 메소드에 대해 지정을 해주는 것이다. 기본적으로는 왼쪽이 동작의 방식을 확인하기는 더 쉽다. self는 해당 기호가 사용될 때 왼쪽에 위치한 항을 나타내고 other은 그 반대이다. 이게 기본이나 앞에 r이 붙은 특수 메소드들은 그 위치가 반대이다! 이것은 다음 단계에서 보게 될 것이다.

어떻게 하든 간에 당장의 결과는 달성된 것으로 보인다!
밑러닝-21. 연산자 오버로드(2)
위에서 간단한 수준의 연산자 오버로드를 만들었다. 그러나 우리는 숫자와 변수 객체의 합이나 나눗셈, 빼기 같은 순서가 중요한 연산에 대해서도 구현을 하고 싶다! 일단 이번 단계에서는 타입이 다른 변수의 연산이 가능해지도록 하는 일을 먼저 한다.
일단 변수 객체와 ndarray 객체를 같이 쓸 수 있도록 하자. 간단하다! ndarray가 있으면 그것을 변수 객체로 만들어버리면 된다. 연산자를 쓰는 것은 엄밀하게 말하여 하나의 함수 객체를 쓰는 것임에 유의한다면, 함수 부분 코드를 수정하여 변수 객체를 받아들이게 할 수 있다는 것을 알 수 있다.

간단하게 as_variable을 만들어서 무조건 변수 객체로 감싸는 함수를 만들고, 이를 call할 때 처음부터 전처리 과정으로 넣어준다.
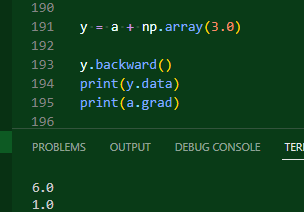
그러면 이렇게 ndarray를 사용하는 것이 가능해진다!

ndarray에서 한술 더 떠서 그냥 일반 float이나 int 자료형의 변수도 가능하도록 바꿔보자. 간단하게 함수를 쓸 때 들어가는 녀석들을 ndarray로만 바꿔주면 알아서 __call__이 일어날 때 변수 객체로 감싸지게 될 것이다. 이때 왜 x0에 대해서는 묶어주지 않는가?

이런 문제가 발생하기 때문이다. 문제가 일어나는 경위는 결국 저 + 연산자는 앞에 있는 변수에 대해서 __add__메소드를 호출하기에 그렇다. float와 같은 단순 자료형의 __add__메소드에는 변수 객체와의 연산이 정의되어 있지 않다. 그렇기에 이 다음으로 a 객체에 우항을 self로 삼고 좌항을 other로 삼는 __radd__ 메소드가 자동으로 호출된다. 그런데 이때도 미리 구현되어 있지 않았기 때문에 작동하지 않는다.
결국 좌항을 as_array하려고 해봤자 먼저 이 부분에서 걸린다는 게 화근인 것이다.
이를 해결하려면? radd 메소드를 만들면 되지!

간단하다!

그렇다고 아직 문제가 전부 해결된 것은 아니니.. 좌항이 ndarray인 경우는 어떻게 할 것인가? 몇가지 실험을 위해 조금 코드가 길어졌는데, 결국 에러가 난 부분을 보면 backward를 치는 부분에서 난 것을 확인할 수 있다. 즉 연산은 잘 이뤄졌는데 그게 ndarray 상의 연산이라 다른 결과가 도출된 격이다. 이런 경우 우리는 ndarray의 연산보다 우리의 변수 객체가 먼저 연산되도록 해줄 필요가 있다. 우선순위를 지정하는 것이다!

이렇게만 해주면 된다고 한다.
밑러닝-22. 연산자 오버로드(3)
이제 연산자 오버로드에 대해서 알아야할 기본 개념들은 전부 안 셈이다. 남은 할 일은 나머지 연산자들도 오버로드 해주는 것. 뺄셈과 나눗셈, 거듭 제곱 등등. 다음과 같은 순서로 만들어주면 된다.
Function 클래스를 상속하는 함수 클래스 만들기
파이썬 함수로 사용할 수 있도록 하기
Variable 클래스에서 연산자를 오버로드하기

앞에 음의 부호를 붙이는 것, 그리고 뺄셈에 대한 설정. 더하기나 곱하기의 경우 순서가 상관없지만, 뺄셈이나 나눗셈은 위치가 매우 중요하다. 그래서 self와 other의 위치가 바뀌는 r의 경우에 대해 따로 함수를 만들어준다.
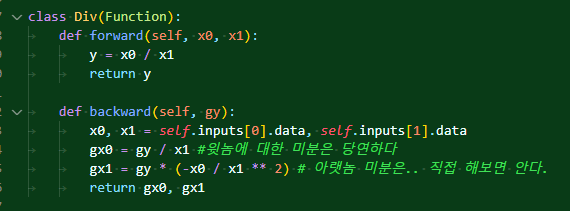
나눗셈도 뭐.. 마찬가지. 나눗셈에 대한 미분 생김새는 알아둬야 만들 수 있는 코드라 따로 빼놨다.

거듭제곱 역시 구현되는데, 생긴 방식은 간단하나 지수 부분에 대한 미분은 고려하지 않는 것으로 한다. 덕분에 구현은 이런 식으로 돼야만 한다. 지수에 들어갈 c가 불필요하게 변수 객체로 싸여 들어가거나 미분의 대상이 되지 않도록 하기 위해 init에서 들어가도록 만들어진다.
밑러닝-23. 패키지로 정리
모듈 - 파이썬 파일을 말한다. 간혹 우리는 한 py파일을 import해서 쓰곤 하는데, 이를 모듈이라 부른다.
패키지 - 이런 모듈들을 한데 묶어놓은 디렉터리이다.
라이브러리 - 이런 패키지를 묶어놓은 디렉터리이다. 하나로 구성된 라이브러리도 있는 법이기에 실상 패키지나 라이브러리는 엄밀하게 구분하여 사용하지는 않는다.
뭐.. 이런 구분은 있지만 실상 어차피 우리는 임포트해서 사용하는 것이 전부라 엄밀한 용어 구분이 불필요한 것 같기는 하다. 실제로 이렇게 정확하게 개념을 구분지어서 사용하지도 않는 것 같고.

이제 너무나도 길어져 버린 우리의 코드를 모듈화 시킬 때가 온 것이다. 모듈화를 시켜 패키지로 정리를 하자!

이제는 길어져버린 우리의 코드를 사가세요.. 먹기 좋게 init까지 해둔다. 이러면 나중에 임포트를 할 때 해당 디렉 이름만 명시를 해주면 된다. init과정이 없으면 core_simple이라는 파일 이름까지 명시를 해줘야만 한다. 이전 파이썬 버전에서는 init파일이 없으면 작동조차 하지 않았다고 한다.

자세한 과정은 생략. 그냥 코드를 옮기는 일밖에 없다. 아무튼 그보다는 이 부분이 중요해보인다. 그냥 python으로 파일을 실행시키면 __file__ 경로가 생긴다고 한다. 여기에 파일 경로를 더 추가하여 dezero 디렉 어디에서든 import를 가능하게 한다.
밑러닝-24. 복잡한 함수의 미분
벤치마크용 함수들을 간단하게 쓰면서 우리의 dezero가 잘 작동하는지 보자!

sphere, 마차시? goldstein-price 함수를 구현하고 각각을 확인하는 과정.

전부 제대로 나오고 있는 모습이다.
밑러닝-25. 계산 그래프 시각화(1)
우리는 이제 고차 미분을 할 것이다. 그것이 무엇인지는 나중에 보고, 일단 이제는 계산 그래프를 시각적으로 표현하는 것을 구현해보자. 바로 graphviz를 이용할 것이다.

일단 잘 설치가 된 것 같다.
윈도우에서 설치할 경우 홈페이지에 가서 파일을 설치하고, 이후에 conda 환경에서 또 설치를 해줘야 하는 모양이다. 찾아보니 글이 좀 많은데, 뭔가 고통을 받은 사람이 많은 모양. 설치하는 것은 잼병이기도 하고.. 시간을 너무 많이 소모할 것 같아서 그냥 나와있는 글에 충실했다.


혹시나 유용한 툴이 있을까 하고 봤는데, 바로 preview를 띄워줄 수 있는 기능이 있다. 근데 disgraph가 아니라 그냥 graph를 쳐야 하는데, 이건 버전 차이인 것일까?
아무튼 이것을 사용하면 내가 저장하기도 전에 변경사항을 볼 수 있다. ctrl +k, 이후 v를 누르면 띄울 수 있는 창.
DOT Language | Graphviz ㅂㄷㅂㄷ.. 책에 있는 거 그대로 치는데 자꾸 안 돼서 결국 공식문서까지 들어갔다. 쓰면서 알게 됐는데, 내가 여태 disgraph라 쓸 때 안 되는 이유는 s를 넣었기 때문이었다..

이렇게 하는 거였구나..
밑러닝-26. 계산 그래프 시각화(2)
dot 언어를 어떻게 쓰는지는 대충 배웠으니, 이제는 우리의 코드가 바로 시각화가 되도록 만들어보자.

변수 객체에 대한 그림을 찍는 부분. 이름이 없으면 ' '로 나타낸다. verbose를 넣으면 해당값도 같이 출력되게 된다. id는 해당 객체의 고유한 id이다.

함수 부분에서 화살표를 잇는 작업을 한다. output은 약한 참조가 걸려있으니 저렇게 작성해야 한다!

다음으로 위에 만든 함수를 쓰는 최종 함수! 변수 객체에서 backward하는 것과 별반 다르지 않다. 그러나 세대를 고려할 필요가 없어서 해당 관련 코드가 빠졌다. 이미 본 변수인지 따져가면서 추가를 시킨다. 이 함수는 적절한 dot 언어로 바꿔주는 작업을 한다.

이제 dot 언어를 만들었으면, 이를 파일로 만드는 작업을 하는 함수도 만들어야지. 일단 해당 언어 파일을 홈 디렉에 숨김 디렉으로 만들고, 이를 활용해서 명령어를 만든다!
새로 보는 함수들이 조금 있는데, splitext는 그냥 확장자와 파일명을 분리하는 명령어라고 한다.
subprocess는 쉘 명령어를 쓸 수 있게 해주는 라이브러리. 그 속에 run이 주되게 쓰이는 모양이다.

여하튼 맛깔나게 그림을 그릴 수 있게 됐다!

주피터파일에서도 원활하게 출력이 되도록 이런 명령어도 써넣는다. 책에서 나온 부분을 보고 그대로 베껴넣은 부분.
밑러닝-27. 테일러 급수 미분
테일러 급수를 통한 미분을 알아보자.
[미적분] 삼각함수 미분: sinx 미분 증명; cosx 미분 증명; sinx 도함수 증명; cosx 도함수 증명; 삼각함수의 도함수 : 네이버 블로그 (naver.com) 일단 sin함수에 대한 미분은 cos이다. 거꾸로는 -가 붙는다!

일단 단순하게 나타낸 모양. 45도에 대하여 미분을 하면 같은 값이 나오게 된다! 그래프 상에서 겹치는 지점.
다르게 미분을 하는 방법이 있다. 바로 테일러 급수를 활용한 미분이다. 테일러 급수란 어떤 함수를 다항식으로 근사하는 방법을 말한다. 엄밀하게 이야기해서 테일러 급수는 무한으로 차수를 보내기에 유한한 항으로 이뤄지는 다항식과는 맞지 않는다는 듯? 아무튼 테일러 급수는 특정 지점에서 해당 함수에 접하는 무한한 항을 통해 표현하는 것이라는 듯하다. 대체로 0을 지점으로 많이 쓰며 이렇게 쓸 때 매클로린 전개라고 부른다.

계속 도함수를 파내려가면서 전개하는 방식. 여기에 a는 0, f에는 sin함수를 넣으면 어찌 되는가?
$\large sin(x) = \frac{x}{1!}-\frac{x^3}{3!}+\frac{x^5}{5!}... = \sum_{i =0}(-1)^i\frac{x^{2i+1}}{(2i+1)!}$
이런 식으로 매우 간략해진다. sin(0)은 0이고 cos(0)은 1이기 때문에 이렇다.

테일러 급수를 활용한 방식. 도출되는 값이 거의 흡사한 것이 보인다. 무한을 표현할 수 없기에 코드적으로는 임계값을 둔다.
테일러 급수가 나오는가? 아마 이후 단계에서 설명이 되겠지.. 일단은 넘어가보자.
밑러닝-28. 함수 최적화
이번에는 최적화를 할 것이다. 최적화가 뭐냐? 어떤 함수가 주어졌을 때 이 함수의 최대값, 혹은 최소값을 내어주는 입력값을 찾는 것이다. 신경망에서 흔히 수렴점을 찾아가는 일을 최적화한다고 부른다. 최적화 함수, optimization이런 표현들을 생각하면 될 것 같다.

최적화가 잘 되는지 확인하기 위한 벤치마크용 함수. 놀랍게도 이 함수는 정말 순수하게 최적화 알고리즘을 시험하기 위해서 탄생한 함수라고 한다. 분명하게 골짜기가 있기에 최소값이 존재한다. 그러나 갈수록 그 기울기가 완만해져서 빠르게 찾는 것이 매우 어렵다고 한다.

엄밀하게 상수를 a,b로 두지만 통상적으로 a는 1, b는 100으로 두고 쓴다고 한다. 이때 최소값은 0으로 (1,1)에서 나온다.

0, -2에서 차근차근 나아가보자. 해당 위치에서의 미분값은 무얼 뜻하는 것인가? 이제부터 본격적으로 딥러닝에서 나오는 개념들에 가까이 다가가고 있다. (-2, 400)이란 미분값은 기울기 벡터라고도 불린다. 이 값은 해당 함수의 해당 지점의 기울기를 뜻하고, 이것은 어디로 가야 내려가고 올라가고를 알려주는 지표라고 할 수 있다. 가령 이 값을 빼서 x값을 업데이트하면 x는 점차 0, -2에 가까이 가게 될 것이다. 그게 바로 우리가 잘 아는 경사하강법이 아닌가!
복잡한 함수라면 당장의 해당 지점에서 기울기를 따라 이동한다고 하여 무조건 해당 함수의 최소값으로 간다고 할 수는 없다. 괜히 local minimum 문제가 있는 게 아니다! 그러나 아무튼 해당 기울기에 충실하게 이동할 수는 있다. 그리고 그러다보면 어떤 식으로든 어떤 끝단 값에 이를 수 있다. 이것이 바로 경사하강법의 기본이다. 우리는 이것을 통해 loss를 최소화시킨다.


경사하강법을 간단하게 구현한 모습. 미분값은 단순하게 대입이 아니라 +되는 방식이기에 꼭 한번의 미분이 일어난 뒤에는 cleargrad를 해줘야만 한다. 나중에는 이게 no_grad가 되어버리겠지.
미분을 진행한 뒤에는 각 x에 대해 미분값이 생길 것이다. 그렇다면 그것을 통해 x의 값을 갱신한다.
zero_grad를 하고, backward를 친다. 그리고 optimizer로 업데이트를 한다.. 이거 어디에서 많이 봤다? 이제 이쪽 분야 공부를 하면 모를 수가 없는 그 과정이 전개되고 있는 것이다.

책에서는 에폭을 10000까지 늘려서 재차 진행하여 결국 최소점으로 수렴한다는 것을 보인다.

그러나 나는 오래 걸리기도 싫고 그냥 빨리 학습만 시키면 될 것 같다고 생각해서 학습률에 손을 댔다가 조금 낭패를 봤다. 해당 함수가 왜 최적화를 위한 벤치마킹용인지 알 것 같다. 진짜 엄청 민감하다. 위는 0.003으로 했을 때의 결과인데, 1,1로 가지를 못한다. 내가 여태 얼마나 학습률에 대해서 안일하게 생각하고 있었는지 체감이 된다. 처음에 단순하게 0.01로 했다가 에러가 나길래 뭔가 했네..

그래도 0.002까지는 괜찮은 수준인가보다. 0.001로 했을 때는 10000번으로 부족한데, 그래도 0.002로 하니까 원하는 정도까지는 나와주는 듯하다.
밑러닝-29. 뉴턴 방법으로 푸는 최적화(수동 계산)
10000이나 돌아야한다니. 그러면서도 완벽하게 수렴을 하지 못한다니. 우리는 이를 개선할 수 있다! 이를 해결하는 좋은 방법 중 하나가 바로 뉴턴 방법이다. 50000번 가량 걸리는 계산을 6번만에 끝낼 수 있는 대단한 놈이다!
여기에서 바로 테일러 급수가 등장한다. 테일러 급수는 차수를 높이며 미분한 값으로 해당 식을 표현한다는 데에 핵심이 있다. 자세한 설명은 책에서 참고.. 요지는 미분의 미분의 미분의 미분..의 미분을 활용하면서 얼마나 업데이트를 하는 것이 좋은지 함수에서 도출할 수 있다는 것이다.
$\large x -= \alpha f'(x)$
$\large x -= \frac{f'(x)}{f''(x)}$
위가 경사하강법, 아래가 뉴턴방법이라고 볼 수 있다. 참고로 아래는 2차 미분만 적용하여 뉴턴 방법을 활용한 것. 원래는 인간이 수동으로 조절해야 했던 하이퍼 파라미터 알파가 미분의 미분값으로 대체된 꼴이다. 자동으로 학습률을 바꾼다! 이러니 함수가 뻑이 가지...

우리는 아직 2차 미분 등의 방식을 자동으로 가능하게 할 방법이 없다. 이번 장에서 이게 우리가 할 목표지! 고차 미분 자동화.. 아무튼 지금은 못하니까 그냥 손으로 2차 미분을 한 값을 함수로 만들어서 넣어준다. 몇 번 걸리지 않아 곧바로 수렴점으로 이동한 것이 확인된다.
이 좋은 것을 빨리 자동화해보자고!
밑러닝-30. 고차 미분(준비 편)
장차 고차 미분을 하려면, 현재의 코드를 부득이하게 바꿔야만 한다. 어떻게 해야 하나? 현재의 코드를 돌아보자.
변수 객체에는 두 개의 값이 담긴다. 해당 값 그 자체, data와 그것의 변수의 미분값에 해당하는 grad. grad는 처음에 None이지만, 이후 역전파가 진행됨에 따라 값이 채워지는 구조이다.
함수 객체에서는 변수와의 연결을 이룬다. 순전파를 쭉 하고, 이후에 출력된 값의 창조 함수로 자신을 설정한다. 그 후에는 자신 속에 입력 변수와 출력 변수를 저장한다. 이는 미분을 역방향으로 흘려보내기 위해 값을 기억해두는 것이다.
나는 아직 무얼 하려는지 잘 모르겠다.. 일단 닥치고 따라가야지
밑러닝-31. 고차 미분(이론 편)
결국 요점은 뭐냐? 계산의 연결은 함수의 __call__끝자락에서 이뤄진다. 구체적인 역전파는 함수의 forward와 backward를 통해 이뤄진다.
여기에 핵심이 있다. 계산 그래프의 연결은 순전파를 할 때 만들어진다. 역전파를 할 때는 만들어지지 않는다! 역전파 시에는 ndarray를 통한 계산만 이뤄지는데 이때 여기에서도 연결이 발생한다면 고차 미분 자동화가 가능해진다!

이건 순전파 시의 sin함수 계산 그래프이다.

역전파 시의 그래프를 나타내보았다. gx를 구하기 위한 과정! gx = gy * cos(x)라는 식을 이렇게 표현해낸 것이다. 이러한 표현식이 있다면 어떤 게 가능해지는가? 2차 미분이 가능해진다. 이 그래프에서 gx.backward()를 칠 수 있다면, 이는 2차 미분이 되는 셈이다. 그렇기에 우리는 이 그래프가 우리 코드 상에서 작동할 수 있도록 연결을 만들어주는 것이 목표가 되는 것이다.
그 방법은 의외로 간단하다. gx, 즉 미분값을 변수 객체로 만들어주면 된다. 물론 조금은 더 수정을 가해야 하지만, 아무튼 따지자면 x.data를 가지는 변수 객체의 x.grad를 변수 객체로 만들면 된다는 것. 그럼 그 해당 객체는 data로 x.grad를 가질 것이고, x.grad.grad에 2차 미분값을 담을 공간을 마련하게 될 것이다.
조금 더 정확하게 말하자면 계산을 하는 시점에서 계산 그래프가 연결된다(그래서 순전파 때 역전파를 위한 연결이 이뤄지는 것). 그런데 여태의 backward 과정에서 사용되는 값들은 죄다 ndarray였다. 근데 이것들이 변수 객체로 바뀌는 순간, backward에서 이용되는 모든 연산 기호와 연산들이 변수 객체에서 사용되는 연산으로 의미가 바뀐다는 뜻이다. 즉, 역전파 때도 변수 객체로 연산을 하게 되면 연결이 이어지는 것이다. 그래서 미분값을 변수 객체로 만들면 된다는 것이다!
라이트닝4
저번에 잘못 봐서 제대로 하지도 못했던 4부터. 4단계는 arg을 쓰는 방법에 관한 내용을 담고있다. 근데 이건 레거시라고 위에서 바로 경고를 띄워주더라. 혹시나 해서 봤는데, 이후 단계에서 lightning cli에 관한 내용이 또 나오는 것을 확인했고, 그래서 어차피 이후에 다시 배울 것이라 감안하고 이 내용을 그대로 진행했다.

이 놈을 데코레이터 씌워서 사용한다는 듯.

결국 사용할 때는 인자로 받아서 사용하는 것 같다.

그것보다 핵심은 이것. 각 함수에서 쓰이는 인자를 정말 인자로 추가할 수 있게 만든다.

보다시피 이상한 인자들을 쓸 수 있게 되었다!
라이트닝5
5의 내용은 디버깅과 시각화에 관련한 내용이다.

트레이너에 빠르게 런하는 옵션이 있는데 이것을 넣으면 체크 포인트나 얼리스타핑 무시하고 일단 빠르게 5번 돌면서 테스트, 검증, 학습 전부 진행해본다고 한다. 말그대로 코드 상 버그를 찾기 위함.

..? 막상 넣으니까 5번도 안 도는데.. 이제보니 5 배치를 돈다는 것이었다.

이런 식으로 적당히만 돌도록 데이터량을 조절하는 방법도 있다. 에폭은 에폭대로 돌되, 도는 배치량을 자르는 것이다.
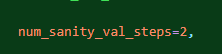
이걸 넣어서 일단 배치가 제대로 돌아가는지 확인을 하는 방법도 있다. 이건 정말 돌아가는지만 확인하는 용인 것 같다. 근데 왜 굳이 있는지는 모르겠다.

valid step에만 출력문을 넣어서 확인했다. 이름 말마따나 확실하게 valid에 대해서 진행한다.
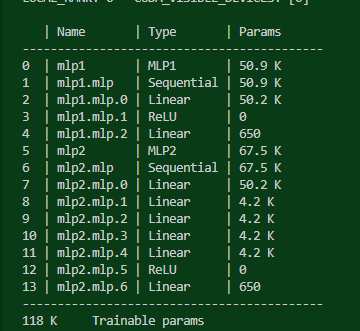
modelsummary를 callback에 넣으면 생기는 일. 자식 모델까지 전부 보여준다!

fit이 없는 상태에서 저것을 보여주고 싶다면 이렇게 쓰면 된다고 한다.

이제는 병목 현상 해결하는 방법에 대해. 트레이너에 profiler를 사용해서 병목이 일어나거나 오래 걸리는 녀석이 뭔지 알 수 있다. simple로 하면 이 정도고..

뭔가 난장판을 피울 수도 있다. 스크롤이 끝이 없네..

터미널로 보기 짜증나는 나같은 사람을 위해 파일로 남기는 방법까지 제공한다.
이게 시각화 방법! 5단계 내용 왤케 많은 거야 ㅠ

그니까 라이트닝은 다양한 형식으로 데이터를 표현해줄 수 있고 내 빈약한 상상력과 창의력이 방해 요인이라네!

뭔가 시각화를 시켜준다는 것 같아서 활용해보려고 했으나, 어떻게 해야 하는지 잘 모르겠다. 정말 내 상상력이 빈곤하긴 한가보구나!
근데 아무런 변화가 없어서 일단 스톱.. 본인들이 어떤 식으로 나온다고 보여주기라도 해야지 코드만 띡 두면 어떻게 나와야 정상인지 어케 아냐.
웹페이지로 띄우는 방법도 있다는데 이건 텐서보드를 활용하는 것이라 패스했다.
스터디
웹페이지로 띄우는 것은 가뿐히 포기했는데, 막상 텐서보드를 깔아보니 정말 간단했다. 텐서보드 자체가 생소해서 함부로 손을 못대는 측면이 없잖아 있는데, 조금 사용법을 익히면 유의미하게 활용할 수 있을 것 같기도..
Leetcode Weekly Contest
2500 Delete Greatest Value in Each Row - LeetCode
양의 정수로 이뤄진 m * n 행렬이 주어진다. 이 행렬이 비워질 때까지 다음의 동작을 한다.
각 행의 가장 높은 값을 없앤다. 중복이 있으면 하나만 지운다. 지워진 놈 중 가장 큰 놈을 정답에 더한다.
한 칸을 지워버리니 한 차례마다 한 열이 줄어드는 꼴이다. 행렬을 완전히 없애버렸을 때 나오는 정답을 구하라.
import numpy as np
class Solution:
def deleteGreatestValue(self, grid: List[List[int]]) -> int:
answer = 0
lst = np.sort(np.array(grid), axis=1)
for _ in range(lst.shape[1]):
answer += np.max(lst[:,-1])
lst = lst[:,:-1]
return answer쉬움. 프로그래머스에서도 numpy를 쓰는 게 가능했던 것이 기억나서 한번 시도해봤는데 잘 된다. 좋은 게 있으면 활용하지 않을 이유가 없다. 또한 numpy 자체를 다루는 걸 많이 해본 적이 없어서 조금 다루는 연습도 할 겸 더 쓰려고 노력했다.
2501 Longest Square Streak in an Array - LeetCode
정수 배열을 받아서 부분집합을 추출하라. 이때 부분집합은 최소 2개의 원소를 지녀야 하고, 정렬을 했을 때 원소가 갈수록 제곱이 되는, square streak을 달성해야 한다.
가장 긴 square streak의 길이를 반환하라. 안 만들어질 시에는 -1을 반환하라.
class Solution:
def longestSquareStreak(self, nums: List[int]) -> int:
self.ans = 1
nums = set(nums)
def recur(lst):
self.flag = False
tmp = []
for i in lst:
sqrt = i ** 2
if sqrt in nums:
tmp.append(sqrt)
self.flag = True
if self.flag:
self.ans += 1
recur(tmp)
recur(nums)
if self.ans == 1: return -1
else: return self.ans어려움. 처음에 문제 접근을 어떻게 해야 할지 많이 헤맸다. 생각했던 아이디어는 문제의 숫자 제한이 10만이라 316 제곱까지가 10만 이하라 그것으로 뭔가를 해보려 했었고, 두번째로는 10만 이하에서 아무리 긴 streak이 생겨도 결국 2의 제곱으로 나아갈 테니까 도출할 수 있는 정답이 최대 16이라는 것으로 뭔가를 해보려 했었다.
근데 죄다 뭔가를 해보려고만 하다가, 마땅한 해결점을 찾지 못하고 헤매다가 머릿속에 잘 안 그려지지만 뭔가 재귀를 통해 풀 수 있을 것 같아서 도전해서 겨우 통과했다.

간혹 보는데 이게 무얼 뜻하는 걸까? 높을수록 좋은 것인가? 속도는 빨랐는데 메모리는 개차반이다?
2502 Design Memory Allocator - LeetCode
0으로 인덱스가 시작하는 메모리를 대표하는 n 정수를 받는다. 나는 메모리 할당을 할 수 있다.
Allocator 클래스를 만들어라. init에서는 메모리 할당을 진행한다. allocate에서는 size만큼의 자리에 mID를 할당한다. free는 받은 mID를 해제해주면 된다. 할당은 왼쪽부터. 자세한 건 문제 참조. 일일히 적기 귀찮다..
class Allocator:
def __init__(self, n: int):
self.n = n
self.lst = [-1 for _ in range(n)]
def allocate(self, size: int, mID: int) -> int:
for i in range(len(self.lst)):
if self.lst[i] == -1:
self.flag = True
for j in range(size):
if i+j >= self.n: return -1
if self.lst[i+j] != -1:
self.flag = False
break
if self.flag:
for j in range(size):
self.lst[i+j] = mID
return i
return -1
def free(self, mID: int) -> int:
count = 0
for i in range(len(self.lst)):
if self.lst[i] == mID:
self.lst[i] = -1
count += 1
return count어려움. 처음에 문제 이해를 하는데 시간을 좀 먹었다. 풀이는 맞는 것 같은데, 이렇게 하면 시간 초과가 난다. 조금만 더 고민하면 더 좋은 해결법을 찾을 수 있을 것 같은데, 이정도만 고민하고 넘어가련다.
면접을 위한 CS
2.2 TCP/IP 4계층 모델
인터넷 프로토콜 스위트 - 인터넷에서 컴퓨더들이 서로 정보를 주고받는 데 쓰이는 프로토콜의 집합.
이를 TCP/IP 4계층 모델이나, OSI 7계층 모델로 설명한다.

현재 기준으로 4계층이 보편화되어 있는 모양이다. 신뢰성이 우수하고 개방성이 있다. 책에서는 4계층 중점적으로 설명한다. OSI 7 Layer 과 TCP/IP 4 Layer(TCP/IP Protocol suite) 비교 (tistory.com)
4계층에서 눈여겨 볼 점은 계층이 단순화되어 있고, 네트워크 층을 인터넷 층이라 부른다는 점. 이 계층들은 각 계층을 바꿔끼워도 문제가 발생하지 않는다.

각 계층 별로 스택이 다양하다. 책에서 나오는 것과 또 다르길래 가져와봤는데, 나는 자세한 것은 잘 모르겠다. 몇 개는 그래도 어디선가 봤던 기억이 난다.
아무튼 한 계층씩 보자.
애플리케이션 계층
응용 프로그램이 사용되는 프로토콜 계층. 웹이나 이메일 등 실질적으로 사람들에게 서비스가 제공되는 층이다.
- FTP - 장치와 장치 간의 파일을 전송하는 데 사용되는 표준 통신 프로토콜
- SSH - 보안되지 않은 네트워크에서 네트워크 서비스를 안전하게 운영하기 위한 암호화 네트워크 프로토콜. 이건 vs코드를 쓰면서 많이 쓰게 된다. 비단 그게 아니더라도 깃을 연결할 때 원격키를 만드는 경우와 종종 있다.
- HTTP - World Wide Web을 위한 데이터 통신의 기초이자 웹 사이트를 이용하는 데 쓰는 프로토콜. 이거 더 나아가면 HTTPS라고 보면 되겠지? 사설키니 대칭키니 쓰는 그것..
- SMTP - 전자 메일 전송을 위한 인터넷 표준 통신 프로토콜
- DNS - 도메인 이름과 IP 주소를 매핑해주는 서버. IP주소가 바뀌더라도 똑같은 도메인 주소로 서비스할 수 있다. 네이버에서 하위 사이트로 들어가더라도 계속 네이버로 이름이 유지되는 그 원리를 말하는 듯하다.
전송 계층
송신자와 수신자를 연결하는 통신 서비스를 제공한다. 중간 계층 역할로 데이터를 전달할 때의 중계 역할을 한다.
대표적으로 TCP, UDP가 있다.
TCP - 패킷 사이의 순서를 보장. 연결지향 프로토콜. 수신 여부를 확인하면서 가상 회선 패킷 교환 방식을 사용한다.
UDP - 순서를 보장하지 않고 , 단순히 데이터만 주는 데이터그램 패킷 교환 방식을 사용한다.
각 패킷 교환 방식이 무엇인지 알아보자.

가상 회선 패킷 교환 방식. 각 패킷에 가상회선 식별자가 포함된다. 모든 패킷이 전송된 이후 가상회선이 해제된다. 보다시피 패킷이 순서대로 도착하는 것을 볼 수 있다.

데이터그램 패킷 교환 방식. 패킷이 독립적으로 이동하면서 최적의 경로를 따라 간다. 지네 맘대로 가는지라 순서가 다르게 갈 수도 있다. 회선이 연결되거나 끊어지는 과정도 없어서 제대로 갔는지 확인도 하지 않는다.
TCP에 대해서 추가적으로. 신뢰성 있는 전송을 위해 3-웨이 핸드쉐이크 방식을 사용한다. 추억돋네..
3단계를 거친다.
- SYN - 클라이언트가 서버에 자신의 ISN(새 TCP 연결에 쓰일 첫 번째 패킷에 할당된 번호)을 담아 SYN을 보낸다.
- SYN + ACK - 서버는 이를 수신하고 자신의 ISN을 보내면서 승인 번호를 클라이언트의 ISN + 1로 한다.
- ACK - 클라이언트는 서버의 ISN + 1한 값을 담은 ACK를 서버에 보낸다.
이런 과정을 통해 신뢰성이 구축된다.
SYNchronization(연결 요청 플래그), ACKnowledgement(응답 플래그), Initial Sequence Numbers
연결할 때는 3이었지만, 해제할 때는 4-웨이 핸드쉐이크이다.
- 클라이언트에서 먼저 FIN으로 설정된 세그먼트를 보낸다. 그리고 FIN_WAIT_1 상태가 되어 서버의 응답을 기다린다.
- 서버는 ACK라는 승인 세그먼트를 보낸다. 그리고 CLOSE_WAIT 상태가 된다. 클라이언트는 잘 받았을 때 FIN_WAIT_2 상태가 된다.
- 서버는 ACK를 보낸 이후 일정 시간 이후에 FIN이라는 세그먼트를 보낸다.
- FIN을 받은 클라이언트는 TIME_WAIT 상태가 된다. 그리고 ACK를 서버에 보내면서 서버는 CLOSED가 된다. 클라이언트는 일정 시간이 지난 후에 닫힌다.
왜 굳이 이렇게 일정 시간을 기다리는가? 지연 패킷이 발생할 경우가 있기 때문이다. 아직 도착하지 못한 패킷이 있을 수 있다는 게 문제인 것. 이것을 서로 확실히 하지 못하면 무결성 문제가 발생한다.
인터넷 계층
장치로부터 받은 네트워크 패킷을 IP 주소로 지정된 목적지로 전송하기 위해 사용되는 계층. IP, ARP, ICMP 등이 있다. 상대가 제대로 받았는지 보장하지 않는다.
링크 계층
전선, 광섬유, 무선 등으로 실질적으로 데이터를 전달하며 장치 간에 신호를 주고 받는 규칙을 정하는 계층.
네트워크 접근 계층이라고도 부른다.
이를 물리, 데이터 링크 계층으로 또 나누기도 한다.
물리 계층은 LAN을 통해 0과 1로 이뤄진 데이터를 보내는 계층, 데이터 링크 계층은 이더넷 프레임을 통해 에러 확인이나 흐름제어를 하는 계층이다.
유선 LAN과 무선 LAN을 보자.
먼저 유선!
전이중화 통신 - 양쪽 장치가 동시에 송수신 가능.
CSMA/CD - 데이터를 보낸 이후 충돌이 발생한다면 일정 시간 이후 재전송
트위스트 페어 케이블과 흔히 보는 UTP 케이블이 있다. 광섬유 케이블도 있는데 레이저를 통해 통신한다. 뭔가 엄청난 과정을 거치는 듯하다..
무선!
반이중화 통신 - 서로 통신은 가능하나 한번에 한 방향만 가능하다. 무전기 생각하면 편할 듯하다.
CSMA/CA - 캐리어 감지 등으로 사전에 충돌을 최대한 방지한다. 데이터 송신 이전에 회선이 비어있는지 판단한다. 이때 랜덤한 시간을 기다리며 만약 다른 무선 매체가 사용 중일 때는 이 시간을 늘리며 기다린다. 그 이후 비면 데이터를 송신한다.
무선 추가 내용.
주파수를 쏘아 망을 구축한다. 2.4GHz, 5GHz 대역하는 게 여기에서 나오는 것인데, 2.4는 장애물에 강하나 간섭이 많이 일어난다. 그럼 뭐가 강하단 거냐?ㅋㅋ
와이파이는 전자기기들이 무선 LAN에 연결할 수 있게 하는 기술이다. 이를 위해 무선 접속 장치(AP)가 필요하다. 다른 말로 공유기! 이런 기술에는 블루투스도 있다.


BSS는 기본 서비스 집합을 말한다. 단순히 공유기를 통해 네트워크에 접속하는 게 아니라, 동일한 BSS 내에 있으면 서로 통신이 가능하다.
ESS는 하나 이상 연결된 BSS 그룹을 말한다.
이제 데이터 링크 계층에서 보는 이더넷 프레임이 무엇인지 확인해보자.

모양은 대충 이레 생겨먹었다.
- Preamble - 이더넷 프레임의 시작을 알림
- SFD - 다음 바이트부터 MAC 주소가 시작됨을 알림
- DMAC, SMAC - 수신, 송신 MAC 주소를 알림
- EtherType - 데이터 계층 위의 IP 프로토콜을 정의함
- Payload - 진짜로 전달하게 되는 데이터
- CRC - 에러 확인 비트
이제 얼추 계층이 어떻게 생겨먹었는지 확인했다. 그러면 실제로 데이터 송수신은 어떻게 되는가?
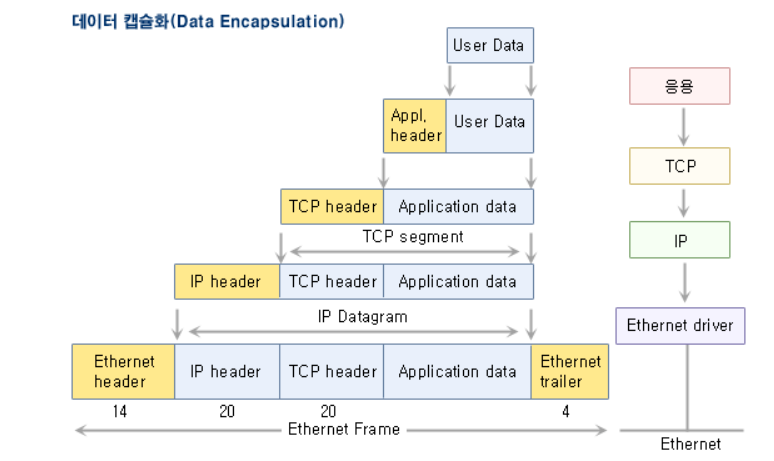
내 컴퓨터에서 4계층을 지나 링크 계층에서 서버 컴퓨터의 링크 계층을 타고 4계층을 올라간다. 이 과정에서 계속 캡슐화가 이뤄진다. 거꾸로 가면 비캡슐화.
응용 계층에서는 메시지라 불리는 데이터가 전송계층에 가게 되면 세그먼트, 데이터그램이 된다. 그 아래로 가면 패킷이 되고, 더 아래로 가면 프레임이 된다.
이렇게 각각의 계층에서의 단위를 PDU라고 부른다.
회고 및 다짐
오늘이 로아온이라는 걸 어렴풋이 알고 있었는데, 막상 오늘이 되자 새까맣게 까먹었다가 집에 갈 때쯤에서야 기억이 났다. 종일토록 할 일이 있었으니 기억 못할 만도 하지. 그래도 집에 와서 빠르게 돌려보면서 내용들을 쭉 훑었는데, 뭔가 그리운 기분이 들었다. 좋은 기억들만 새록새록 피어올랐다. 내가 가장 인상 깊었던 것은 개발진들이 유저들에게 편지를 썼던 부분이다. 커피트럭이나 지하철역 광고 등으로 유저들이 여태 개발진에게 주었던 사랑을 개발진들도 메시지로 화답하는 듯한 느낌이 들어서 무언가 연결되어 있다는 듯한 인상을 준 것 같다. 요즘에는 게임 커뮤니티도 들어가지 않아서 여론이 어떤지는 모르겠지만, 그래도 나는 이런 게임을 좋아했다는 사실을 부끄럽지 않게 해주는 이 게임이 새삼 좋다. 아마 나중에라도 게임에 복귀를 하게 될까? 흠.. 아마 하더라도 스토리나 조금 볼 정도로만 하지 않을까 싶기는 하다. 이제는 그렇게 시간 들여가면서 게임을 하고 싶지는 않다. 아니, 사실 하고는 싶은데 그 시절의 생활로 돌아가기가 싫은 것이다. 하릴 없이 시간 떼우기에 급급했던 수단으로서의 게임을 하고 싶지 않은 것이다.
스토리 보고, 디렉터 보고 시작했던 게임. 디렉터 돌아올 때쯤에 나도 돌아갈 수 있게 더 열심히 해보자고. 정말 돌아갈지는 의문이지만.. 최소한 그런 선택지를 가질 수 있는 나였으면 한다.